1. Speicherung

Bei der Wahl und dem Design eines Algorithmus ist die Speicherung ein großer Faktor. Das Zusammenspiel aus Größe, Kosten und Zugriffszeiten muss berücksichtigt werden, um teure Operationen und Zugriffe zu minimieren. Deshalb befassen wir uns im ersten Kapitel mit der Speicherung sowie unter anderem mit Speicherstrukturen und -hierarchien, um Algorithmen bestmöglich zu designen und effizient einzusetzen.

Zoom in die interne Ebene

Fig. 1.1 5-Schichten-Architektur

Auf der Datenmodellebene können Relationen definiert und die relationale Algebra verwendet werden. Darunter befindet sich die logische Ebene. Auf dieser Ebene kann betrachtet werden, wo die Daten liegen bzw. wie sie verteilt sind. Die nächsten zwei Ebenen beschäftigen sich mit den Speicherstrukturen. Also wo die Daten physisch abgelegt sind und über welche Puffer bzw. Schnittstellen darauf zugegriffen werden kann. Unterhalb dieser Ebenen befindet sich noch eine weitere Schnittstelle zum Betriebssystem. Es gibt zwei Varianten, wie man mit einem Betriebssystem umgeht. Bei der einen Variante versucht man mit dem System zu arbeiten, bei der anderen Variante versucht man es zu umgehen.

1.1. Speicherhierarchie

Die Pyramide zur Speicherhierachie (siehe Fig. 1.2) soll veranschaulichen, wie sich die Kosten, Zugriffszeiten und Kapazitäten der unterschiedlichen Speichermedien verhalten.
In Anbetracht der Kosten sind Archivspeicher sehr günstig verglichen mit Registern, die die teuerste Speicherform in dieser Pyramide darstellen.
Bei den Zugriffszeiten wiederrum ist der Archivspeicher am langsamsten und braucht Sekunden, wenn nicht Minuten. Wohingegen Register sehr schnelle Zugriffszeiten unter 1ns ermöglichen.
In Bezug auf die Kapazität, bietet der Archivspeicher am meisten Speicherplatz. Ein Register hat mit 10kB beispielsweise deutlich weniger zur Verfügung.

~ Zahlen aus dem Foliensatz von Viktor Leis 2019

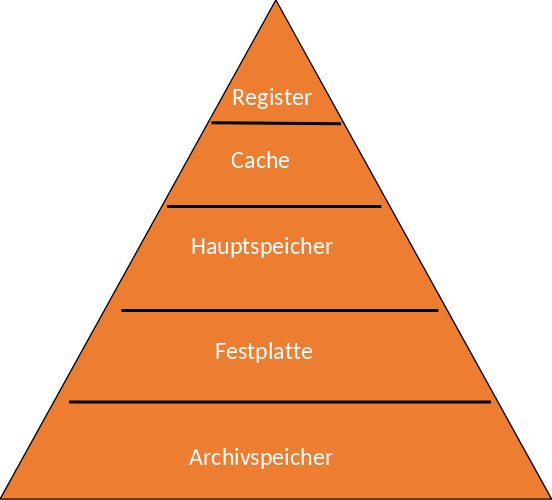
Fig. 1.2 Speicherhierachie

Speichermedium	Kosten	Zugriffszeiten	Kapazitäten
Register	Sehr teuer	< 1ns	10KB
Cache	Sehr teuer	1-10ns	10MB
Hauptspeicher	~ 5€/GB	100ns	100GB
Festplatte	~ 0.05€/GB	SSDs 100us Festplatte 8-10ms	SSDs 5TB Festplatte 50 TB
Archivspeicher	< 1€/GB	sec - min	~ 1PB

1.1.1. Virtueller Speicher

Jede Anwendung verwaltet einen virtuellen Adressraum. Dieser kann größer als der tatsächlich verfügbare Hauptspeicher sein. Mit einem 32-bit Adressraum sind \(2^{32}\) unterschiedliche Adressen darstellbar. Jedes Byte hat dabei eine eigene Adresse. Dadurch lässt sich maximal eine Hauptspeichergröße von 4GB addressieren.
Heutzutage ist der 64-bit Adressraum der Standard. Damit lassen sich maximal 16 Exabyte addressieren. Dies ist deutlich mehr als ein gewöhlicher Computer/Laptop mit 1 oder 2 TB Speicher. Eine 64-bit Addressierung bietet somit noch deutlich mehr Potenzial.
Meistens ist aber deutlich weniger Hauptspeicher als Speicher auf der Festplatte vorhanden. Zur Abhilfe werden die Daten auf eine Disk ausgelagert. Dazu müssen ganze Blöcke (Blockgröße zwischen 4 bis 56 KB) zwischen Hauptspeicher und Festplatte gelesen und geschrieben werden (Seiten des virtuellen Speichers). Es werden nicht einzelne ASCII-Zeichen, sondern ganze Blöcke, die beispielsweise mehrere ASCII-Zeichen enthalten, gelesen. Die Transferzeiten ändern sich nämlich kaum, wenn Blöcke anstelle von einzelnen Zeichen gelesen und geschreiben werden. Es können nicht beliebig viele Zeichen in einem Block sein. Irgendwann ist auch das zu viel.
Die Zugriffe werden durch ein Betriebssystem verwaltet und eingeschränkt. Datenbankensysteme können Begriffe wie ‘O_DIRECT’ verwenden, um doch selbst die Positionen der Daten auf den Festplatten zu verwalten und eigene Bufferpoolmanager zu verwenden. Ein Betriebssystem hat beispielsweise mehrere Anwendungen für die es den Hauptspeicher verwalten muss. Daher kann es sein, dass das Betriebssystem eine Anwendung vorzieht, bevor es die Daten aus der Datenbank bearbeitet.

1.1.2. Sekundärspeicher: Festplatten

Unter Sekundärspeicher fallen nicht nur (magnetische) Festplattens, sondern auch optische (read-only) Speicher. Im Wesentlichen gibt es auf Sekundärspeicher wahlfreien Zugriff (random access). Dabei kostet der Zugriff auf jedes Datum gleich viel, aber dafür muss man dort erst einmal hinkommen!
HDDs halten Daten aus Cache bzw. die Seiten des virtuellen Speichers von Anwendungsprogrammen. Außerdem halten sie Daten aus Dateisystemen.
Es gibt zwei Operationen auf Festplatten. Zum Einem Disk-read. Darunter versteht man das Kopieren eines Blocks in den Hauptspeicher. Zum Anderen Disk-write, dem Kopieren eines Blocks aus dem Hauptspeicher auf die Festplatte. Beides gilt jeweils als eine Disk-I/O-Operation.

1.1.3. Festplatten - Puffer

Ein Bufferpool-Manager puffert Teile von Dateien. In Abbildung 1.3 sehen wir einen Bufferpool-Manager mit einer Blockgröße von 4 KB. Dabei werden immer 4 KB in den Pool geladen. Dieser Block kann dann geschrieben oder auch verworfen werden.

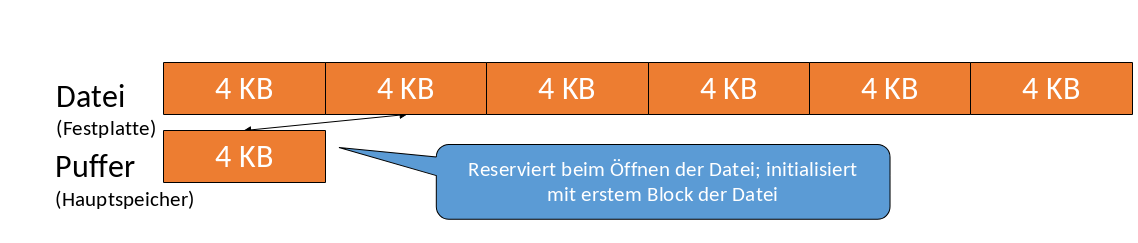
Fig. 1.3 Festplatten-Puffer

Das DBMS verwaltet die Positionen der Blöcke innerhalb der Datei selbst. Dafür ist nicht mehr das Betriebssystem zuständig.
Die Dauer für das Schreiben oder Lesen eines Blocks beträgt 10 bis 30 ms. In dieser kurzen Zeitspanne können viele Millionen Prozessoranweisungen ausgeführt werden. Somit dominiert das Lesen und Schreiben, also die I/O-Zeit, die Gesamtkosten. Die Blöcke sollten daher am besten im Hauptspeicher liegen. Das ist nicht immer möglich, da der Hauptspeicher meist zu klein ist.

Die zuvor genannten Zahlen können je nach Betriebssystem variieren. Sie sind hier aber immer ungefähr im gleichen Skalierungsraum und sollen dabei helfen ein Gefühl für die Zugriffszeiten zu vermitteln.

1.1.4. Tertiärspeicher: Magnetbänder

Tertiärspeicher kann viele Terabyte (\(10^{12}\) Bytes) Verkaufsdaten, sowie viele Petabyte (\(10^{15}\) Bytes) Satellitenbeobachtungsdaten speichern. Für diesen Einsatzbereich wären Festplatten ungeeignet. Sie sind zu teuer aufgrund von Wartung und Strom.
Im Vergleich zum Sekundärspeicher sind zwar die I/O-Zeiten wesentlich höher, aber dafür steigt auch die Kapazität. Ein weiterer Vorteil sind die geringeren Kosten pro Byte gegenüber den Festplatten.
Auf Tertiärspeicher gibt es keinen wahlfreien, sondern zufälligen Zugriff (random access). Die Zugriffszeiten hängen dabei stark von der Position des jeweiligen Datensatzes (in Bezug auf die aktuelle Position des Schreib-/Lesekopfes) ab.

Fig. 1.4 Magnetband

1.1.5. Tertiärspeicher

Ad-hoc können Daten auf Magnetbändern/Magnetbandspulen und Kasseten gespeichert werden. Die Speichermedien werden oft von Menschenhand in die jeweiligen Regale gelegt und geordnet. Daher der Tertiärspeicher in dem Fall gut beschriftet werden. Durch Magnetbandroboter (Silo) kann dieser Prozess ersetzt bzw. optimiert werden. Der Roboter bedient anstelle des Menschen die Magnetbänder (Kassetten). Der Einsatz von Robotern beschleunigt das Verfahren um das zehnfache.
Die Idee ist ähnlich zu CDs, DVDs und Juke-Boxes. Ein Roboterarm extrahiert das jeweilige Medium (CD oder DVD). Der Tertiärspeicher hat wieder eine hohe Lebensdauer von ca. 30 Jahren. Somit ist es wahrscheinlicher, dass kein Lesegerät mehr existiert, als dass der Tertiärspeicher nicht mehr funktioniert.

Fig. 1.5 Tertiärspeicher

1.1.6. Moore’s Law (Gordon Moore, 1965)

Fig. 1.6 Moores Law

Fig. 1.7 Gordon Moore

Moore’s Law beschreibt das exponentielle Wachstum vieler Parameter. Alle 18 Monate findet eine Verdoppelung statt. Zum Beispiel können sich folgende Parameter verdoppeln oder halbieren:

• Prozessorgeschwindigkeit (# instr. per sec.)

• Hauptspeicherkosten pro Bit

• Anzahl der Bits pro cm² Chipfläche

• Diskkosten pro Bit (halbiert)

• Kapazität der größten Disks

Dahingegen kommt es aber zu einer sehr langsamen Verbesserung bei der Zugriffsgeschwindigkeit im Hauptspeicher und der Rotationsgeschwindigkeit von Festplatten, da es physikalisch deutlich schwerer und teurer ist zu realisieren. Als Folge daraus wächst der Latenz-Anteil. Die Bewegung von Daten innerhalb der Speicherhierarchie erscheint immer langsamer (im Vergleich zur Prozessorgeschwindigkeit).

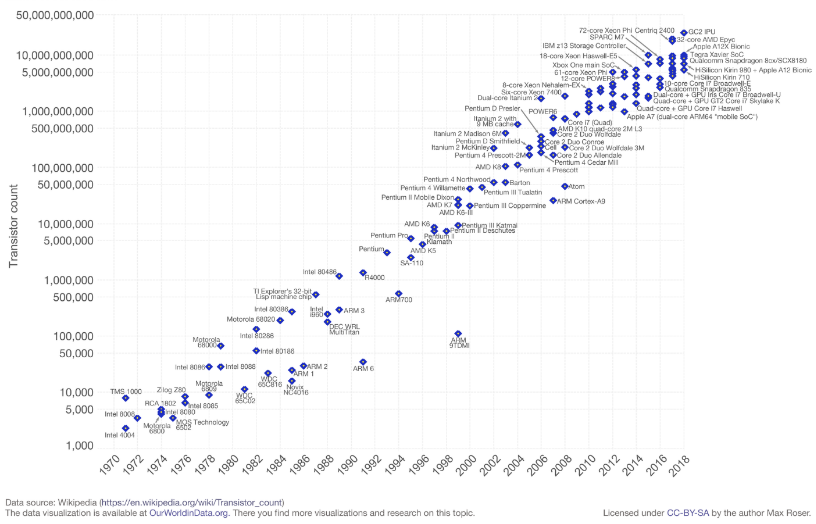
Fig. 1.8 Anzahl Transistoren im Laufe der Zeit

Das Diagramm zeigt die Anzahl der Transistoren als Funktion der Zeit.

Fig. 1.9 1 Gigabyte vor einiger Zeit

Siehe auch: http://www.computerhistory.org/timeline/memory-storage/

1.1.7. Plattenkapazität

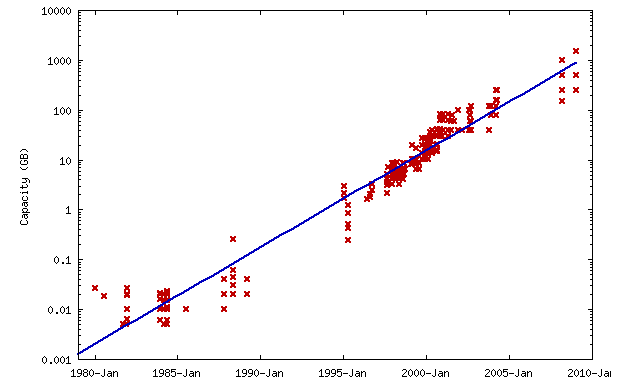
Fig. 1.10 Plattenkapazität

http://en.wikipedia.org/wiki/Hard_disk_drive

Wie man aus diesem Diagramm entnehmen kann, wächst die Plattenkapazität exponentiell.
Die Zugriffszeiten hingegen gleichen sich langsam an. Im folgendem Bild wird der Trend zur maximal anhaltenden Bandbreite gezeigt.

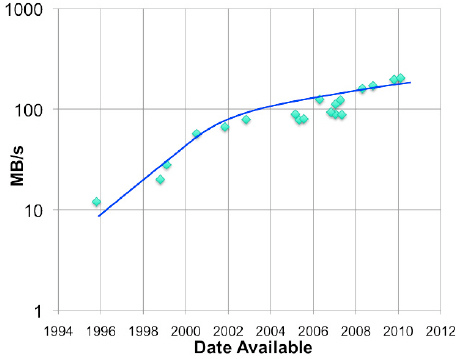
Fig. 1.11 Access Times

Auch die Suchzeiten halbieren sich immer seltener. Daraus ergibt sich der folgende Trend:

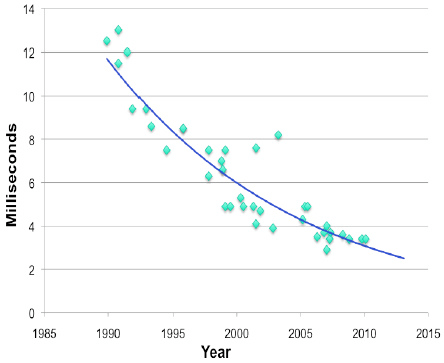
Fig. 1.12 Seek Times

http://www.storagenewsletter.com/news/disk/hdd-technology-trends-ibm

1.1.8. HDDs

Hard Disk Drives (auch kurz HDD genannt) sind eine ältere, aber nach wie vor weit verbreitete Form der Datenspeicher. HDDs verwenden eine magnetische Speicherung auf rotierenden Scheiben, die auch Platten genannt werden.

1.1.9. SSDs

Die persistente Speicherung auf SSDs (Solid State Drive) basiert auf Halbleitern. Es gibt keine mechanische Bewegung oder Rotation wie bei einer HDD-Festplatte. Außerdem bieten SSDs einen hohen Grad an Parallelität.

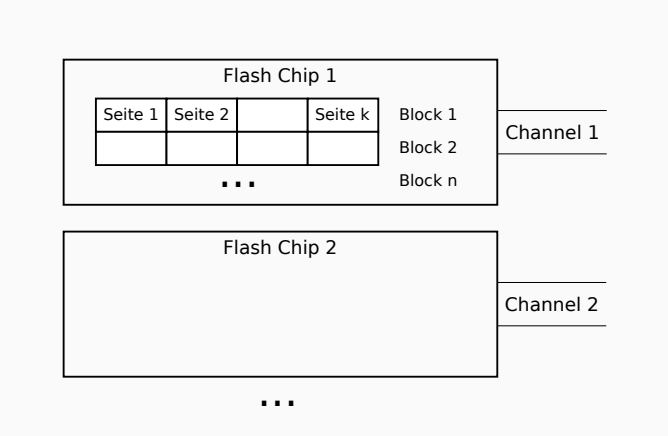
Fig. 1.13 SSDs

1.1.10. HDDs vs. SSDs

Im Vergleich zu HDDs bieten SSDs einige Vorteile:

• Schnelles Hochfahren, da keine Drehung erforderlich ist.

• Schneller Random Access ohne Suchzeiten.

• Geringe Leselatenz.

• Immer nahezu gleiche Lesezeit.

• Keine Probleme durch Dateifragmentierung.

• Stille Operationen und leiser Betrieb.

• Geringer Stromverbrauch.

• Mechanische Zuverlässigkeit.

• Immun gegen Magnete.

• Geringeres Gewicht.

• Parallele Lesezugriffe.

Trotz der wachsenden Beliebtheit von SSDs und ihren Vorteilen bleiben HDDs in verschiedenen Bereichen weiterhin relevant. Grund dafür sind einige Nachteile von SSDs. Diese sollten bei der Entscheidung zwischen HDD und SSD berücksichtigt werden:

• Begrenzte Lebensdauer.

• Datenverlust nach 2-5 Jahren ohne Strom.

• Können nicht defragmentiert werden.

• Teuer.

• Geringere Kapazität.

• Asymmetrische Lese/Schreibgeschwindigkeit aufgrund der Flash-Technologie.

• Leistung von SSDs nimmt mit der Zeit ab.

• SATA-basierte SSDs haben sehr langsame Schreibvorgänge.

• DRAM-basierte SSDs verbrauchen mehr Strom als HDDs.

• Kein sicheres Überschreiben.

Über weitere Vor- und Nachteile können Sie hier weiterlesen.

1.2. Festplatten

Fig. 1.14 Festplatten im Vergleich: Früher und Heute

1.2.1. Aufbau

Eine Festplatte besteht aus mehreren (5-10) gleichförmig rotierenden Platten (z.B. 3.5” Durchmesser). Für jede Plattenoberfläche (10-20) gibt es einen Schreib-/Lesekopf, der sich gleichmäßig bewegt. Die magnetische Plattenoberfläche ist in Spuren unterteilt. Spuren sind als Sektoren fester Größe formatiert, wobei sich die Anzahl der Sektoren pro Spur unterscheiden kann. Übereinander angeordnete Spuren bilden einen Zylinder. Die Platten sind übereinander angeordnet, um Zugriffseffizienz zu ermöglichen. Der Kopf kann parallel auch an anderen Stellen lesen und schreiben.

Fig. 1.15 Aufbau 1

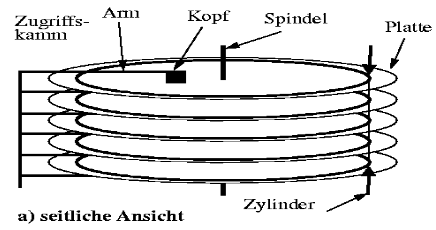
Fig. 1.16 Aufbau 2

Die Sektoren (1-8 KB) sind die kleinste physische Leseeinheit. Die Größe eines Sektors wird vom jeweiligen Hersteller festgelegt. Auf den äußeren Spuren befinden sich mehr Sektoren als auf den inneren. Zwischen den Sektoren existieren Lücken. Sie sind nicht magnetisiert und dienen zum Auffinden der Sektoranfänge. Diese Lücken nehmen etwa 10% der gesamten Spur ein.
Aus den Sektoren lesen wir Blöcke. Blöcke sind die logische Übertragungseinheit. Es ist also die Einheit, die wir auf einmal in den Hauptspeicher laden. Ein Block kann auch aus mehreren Sektoren bestehen.

Fig. 1.17 Aufbau 3

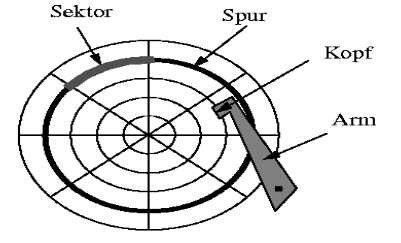
Fig. 1.18 Aufbau 4

Hier in dieser Grafik hat jede Spur die gleiche Anzahl an Sektoren. Normalerweise haben die inneren weniger und die äußeren Spuren mehr Sektoren. Eine Ausnahme wäre es, wenn die Sektoren unterschiedlich groß sind.

1.2.2. Zone Bit Recording

Mehrere Spuren übereinander betrachtet bilden einen Zylinder. Die äußeren Zylinder haben einen größeren Radius und damit eine größere Fläche. Bei gleichen Radien führt dies zu einer (nicht notwendigen) geringeren Bitdichte. Die Lösung sind Zonen mit unterschiedlichen Sektoreinteilungen. Für die folgenden Berechnungen wird dieser Fall vernachlässigt.

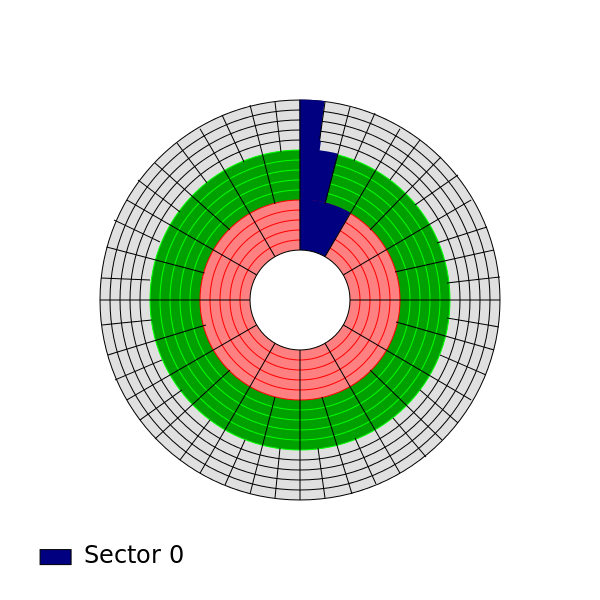
Fig. 1.19 Zone Bit Recording

1.2.3. Disk Controller

Ein Disk Controller steuert eine oder mehrere Disks und die Bewegung der Schreib-/Lese-Köpfe. Außerdem wählt er die Plattenoberfläche aus, auf die zugegriffen werden soll und den Sektor innerhalb der Spur, die sich gerade unter dem Schreib-/Lese-Kopf befindet. Auf diese Weise kontrolliert er den Start und das Ende eines Sektors. Der Disk Controller überträgt noch Bits zwischen Disk und Hauptspeicher und umgekehrt.

Fig. 1.20 Disk Controller

1.2.4. Beispiel - Megatron 747 Disk

Ein Beispiel ist die Megatron 747 Disk mit den folgenden Eigenschaften:

Sie hat 8 Platten mit 16 Plattenoberflächen. Der Durchmesser beträgt 3,5 Zoll. Sie hat \(2^{16} = 65.536\) Spuren pro Oberfläche, durchschnittlich \(2^8 = 256\) Sektoren pro Spur und \(2^{12} = 4.096\) Byte pro Sektor.

Die Gesamtkapazität ergibt sich durch multiplizieren von #Plattenoberflächen, Spuren pro Oberfläche, Sektoren pro Spur und Byte pro Sektor: \(16 x 65.536 x 256 x 4.096 = 2^{40} Byte = 1 TB\). Insgesamt hat die Megatron 747 Disk eine Gesamtkapazität von einem Terrabyte.

Die Blöcke können eine Größe von \(2^{14} Byte (= 16 KB)\) haben. Dann passen 4 Sektoren in einen Block \((\frac{2^{14}}{2^{12}})\) und es gibt im Durchschnitt 64 Blöcke pro Spur \((\frac{2^{8}}{2^{2}})\).

Die Bitdichte für die äußerste Spur wird wie folgt berechnet:

• Bits pro Spur: \(28 \ Sektoren · 2^{12} \ Byte = 2^{20} = 1024 \ KB = 8 \ MBit\)

• Die Spurlänge (äußerste Spur) beträgt \(3,5^“ · p ≈ 11^“\)

• mit ca. 10% Lücken hat man eine Spurlänge von 9,9“, die 8 MBits hält

Somit sind 840.000 Bits pro Zoll vorhanden.

1.2.5. Disk-Zugriffseigenschaften

Eine Voraussetzung für den Zugriff auf einen Block (lesend oder schreibend) ist, dass der S-/L-Kopf auf den richtigen Zylinder positioniert ist, der die Spur mit dem Block enthält. Dann muss die Disk so rotieren, dass Sektoren, die der Block enthält, unter den S-/L-Kopf gelangen.
Hierbei sprechen wir von der Latenzzeit. Sie beschreibt die Zeit zwischen der Anweisung einen Block zu lesen und bis zum Eintreffen des Blocks im Hauptspeicher.

1.2.6. Latenzzeit

Die Latenzzeit setzt sich aus der Summe von vier Komponenten zusammen:

1. Kommunikationszeit zwischen Prozessor und Disk Controller:

   • Sie beträgt nur Bruchteile einer Millisekunde und kann daher bei Berechnungen hier vernachlässigt werden.

2. Seektime (Suchzeit), um den Kopf unter dem richtigen Zylinder zu positionieren:

   • Die Suchzeit ist zwischen 0 und 40 ms ( proportional zum zurückgelegten Weg).

   • Sie setzt sich zusammen aus Startzeit (1 ms), Bewegungszeit (0 – 40 ms) und Stopzeit (1 ms).

3. Rotationslatenzzeit für die Drehung der Disk, bis sich der erste Sektor des Blocks unter S-/L-Kopf befindet:

   • Durchschnittlich benötigt es eine halbe Umdrehung (4 ms) bis der erste Sektor des Blocks unter dem S-/L-Kopf liegt.

   • Eine Optimierung durch Spur-Cache im Disk-Controller ist möglich.

4. Die Transferzeit für die Drehung der Disk, bis alle Sektoren und die Lücken des Blocks unter dem S-/L-Kopf durchlaufen sind:

   • Etwa ein 16 KB-Block in 0.25 ms durchlaufen.

1.2.7. Schreiben und Ändern von Blöcken

Das Schreiben von Blöcken ist in Bezug zu Vorgehen und Zeit analog zum Lesen. Um zu überprüfen, ob eine Schreiboperation erfolgreich war, muss eine Rotation gewartet werden. (Die Nutzung von Checksums wird später beschrieben).

Das Ändern von Blöcken ist nicht direkt möglich. Sondern geschieht in 4 Schritten:

1. Der jeweilige Block wird in den Hauptspeicher gelesen.

2. Die Daten auf dem Block werden geändert.

3. Der Block wird auf die Festplatte zurückgeschrieben.

4. Zum Schluss wird eventuell die Korrektheit der Schreiboperation überprüft

Die Zeit für solch eine Operation ergibt sich aus \(t_{read} + t_{write}\). Mit ein wenig Glück ist der Kopf noch in der Nähe, wodurch t_write billiger wird.

1.2.8. Beispiel – Megatron 747 Disk

Wie lange dauert es, einen Block (16 KB = 16 384 Byte) zu lesen? Diese Frage soll nun am Beispiel der Megatron 747 Disk beantwortet werden.

Die Umdrehungsgeschwindigkeit beträgt \(7200 \ U · min-1\). Somit dauert eine Umdrehung 8,33 ms.

Zunächst wird die Seektime berechnet:
Die Start- und Stopzeit beträgt zusammen eine Millisekunde.
Pro 4000 Zylinder wird 1ms benötigt: - Minimal werden 0 Zylinder übersprungen und man bleibt an der Stelle an der man ist. Dafür werden 0ms benötigt. - Wenn man eine Spur (Track) überspringt, kostet das 1,00025ms (≈1ms). - Maximal werden 65.536 Zylinder übersprungen und das kostet \(\frac{65536}{4000} + 1 = 17,38ms\).

Als nächstes wird die minimale Zeit berechnet, um einen Block zu lesen:
Dafür muss der S-/L-Kopf über der richtigen Spur stehen und die Platte schon richtig rotiert worden sein. Ein Block (16KB) ist über 4 Sektoren und 3 Lücken verteilt. Diese müssen gelesen werden. Insgesamt gibt es durchschnittlich 256 Lücken und 256 Sektoren pro Spur (wurde in vorherigem Unterkapitel so definiert). Die Lücken bedecken 36° (10%) einer Spur. Die Sektoren bedecken 324° des Kreises (360°).
Das Verhältnis wird berechnet mit \(\frac{324° · 4}{ 256} + \frac {36° · 3} {256} = 5,48°\). Es sind also 5,48° des Kreises durch einen Block bedeckt. 5,48° im Verhältnis zur Gesamtrotation (360°) und einer Umdrehung ergeben dann eine Lesezeit von \((\frac{5,48°} {360°}) · 8,33 ms = 0,13 ms\).

Die maximale Zeit zum Lesen eines Blocks wird in der Präsenzübung vertieft. (Kleiner Spoiler: Sie beträgt 25,84 ms). Die durchschnittliche Zeit können Sie selber erforschen und nachrechnen. (Dabei sollten sie auf ungefähr 10,76 ms kommen).

1.3. Effiziente Diskoperationen

Die Kopfbewegungen sollen möglichst minimiert werden, sodass der Kopf nicht die ganze Zeit von Spur zu Spur oder von Block zu Block hin- und herspringt. Dies zieht gewisse Anforderungen mit sich: Zum Einem sollen die Daten auf der Festplatte sinnvoll liegen. Zum Anderen sollte es Indexstrukturen geben, sodass man nicht Suchen muss.

1.3.1. Algorithmen vs. DBMS

Zuvor war die Annahme bei Algorithmen (wie in der Vorlesung ‘Datenstrukturen und Algorithmen’), dass die gesamten Daten in den RAM passen (RAM-Berechnungsmodell) und sie auch bereits dort im Hauptspeicher liegen.

Die Annahme bei der Implementierung von DBMS ist das I/O-Modell. Die gesamten Daten passen nicht mehr in den Hauptspeicher.

Die Externspeicher-Algorithmen funktionieren oft anders. Ein guter Externspeicher-Algorithmus muss nicht der beste Algorithmus laut RAM-Modell sein. Sein primäres Entwurfsziel ist es I/O zu vermeiden.

Das Gleiche kann auch für Hauptspeicher-Algorithmen gelten. Diese nutzen den Cache aus und berücksichtigen die Cachegröße. Es wird versucht die Lokalität zu nutzen und alle fernerliegende Zugriffe zu vermeiden („maximiere“ Anzahl der Cache Hits).

1.3.2. I/O-Modell

Als Beispiel sei ein einfaches DBMS gegeben. Dieses ist zu groß für den Hauptspeicher. Es gibt eine Disk, einen Prozessor und viele konkurrierende Nutzer bzw. Anfragen.

Der Disk-Controller hält und organisiert eine Warteschlange (Priority Queue) mit Zugriffsaufforderungen auf die Datenbank. Das Abarbeitungsprinzip der Zugriffsaufforderungen ist hierbei first-come-first-served. Generell muss angenommen werden, dass jede Aufforderung zufällig ist. Also der Kopf an einer zufälligen Position ist.

Außerdem dominieren die I/O-Kosten. Wir berücksichtigen nicht was im Hauptspeicher geschieht. Die Kosten des Lesens und Bewegens eines Blocks zwischen Disk und Hauptspeicher sind wesentlich größer als die Kosten der Operationen auf den Daten im Hauptspeicher.

Die Anzahl der Blockzugriffe (lesend und schreibend) ist eine gute Approximation der Gesamtkosten und sollte minimiert werden. Anhanddessen kann die Effizienz von Algorithmen beschrieben werden.

1.3.3. Beispiel für das I/O-Modell (1): Indizes

Gegeben sei eine Relation R. Die Anfrage sucht nach dem Tupel t mit dem Schlüsselwert k.
Es existiert ein Index auf dem Schlüsselattribut. Diese Datenstruktur ermöglicht einen schnellen Zugriff auf einen Block, der t enthält. Es gibt zwei Varianten bei Indizes. Die erste Variante gibt nur an in welchem Block t liegt. Die zweite Variante gibt zusätzlich die Stelle von t innerhalb des Blocks an. Die daraus resultierende Frage: Welche Indexvariante ist besser geeignet?

Durchschnittlich benötigt es 11 ms um einen 16 KB-Block zu lesen. In dieser Zeit sind viele Millionen Prozessoranweisungen möglich. Die Suche nach k auf dem Block kostet höchstens Tausende Prozessoranweisungen, selbst mit linearer Suche. Wenn der Block in den Hauptspeicher geladen wurde, sind die Suchkosten darauf verschwindend gering im Vergleich zu den I/O-Kosten.
Die zusätzlichen Informationen (wie der Index zum Beispiel) in Variante B nehmen mehr Platz ein und verursachen höhere I/O-Kosten.

1.3.4. Beispiel für das I/O-Modell (2): Sortierung

Es sei eine Relation R mit 10 Millionen Tupeln und verschiedenen Attributen gegeben. Ein Attribut davon ist der Sortierschlüssel, der nicht unbedingt eindeutig ist. Es ist kein Primärschlüssel. In duiesem Beispiel treffen wir die vereinfachende Annahme, dass der Sortierschlüssel eindeutig ist.

Gespeichert werden die Daten auf Diskblöcken der Größe \(16.384 = 2^{14}\) Byte mit der Annahme, dass 100 Tupel in einen Block passen. Damit wäre die Tupelgröße ca. 160 Byte. R belegt dann 100.000 Blöcke (1,64 Mrd. Bytes) auf der Festplatte.

Es wird eine Megatron 747 Festplatte verwendet. Der verfügbare Hauptspeicherpuffer beträgt \(100 MB (= 100 · 2^{20})\). Somit passen \(\frac{100 · 2^{20}}{2^{14}} = 6400\) Blöcke von R passen in den Hauptspeicher.

Ziel der Sortierung ist es die Anzahl der Lese- und Schreiboperationen zu minimieren und wenig “Durchläufe” durch die Daten zu haben.

1.3.5. Merge Sort

Merge Sort ist ein Hauptspeicher-Algorithmus und fällt unter die Divide-and-Conquer Algorithmen. Die Idee ist es l ≥ 2 sortierte Listen zu einer größeren sortierten Liste zusammenzumergen. Dazu wählt man aus den sortierten Listen stets das kleinste Element und fügt es der großen Liste hinzu.

	Liste 1	Liste 2	Outputliste
1.	1,3,4,9	2,5,7,8	-
2.	3,4,9	2,5,7,8	1
3.	3,4,9	5,7,8	1,2
4.	4,9	5,7,8	1,2,3
5.	9	5,7,8	1,2,3,4
6.	9	7,8	1,2,3,4,5
7.	9	8	1,2,3,4,5,7
8.	9	-	1,2,3,4,5,7,8
9.	-	-	1,2,3,4,5,7,8,9

Die Rekursion bei Merge Sort beginnt mit dem beliebigen Aufteilen einer Liste mit mehr als einem Element in zwei gleich lange Listen L1 und L2. Die Teillisten L1 und L2 werden rekursiv sortiert. Danach werden beide Teillisten zu einer sortierten Liste gemerged.

Der Aufwand von Merge Sort lässt sich in ein paar Schritten berechnen. Die Eingabegröße ist \(|R| = n\).
Das Mergen zweier sortierter Listen L1, L2 kostet: \(O(|L1| + |L2|) = O(n)\).
Die Rekursionstiefe ist \(log2(n)\), da sich in jedem Rekursionsschritt die Listenlänge halbiert. Nach i Schritten sind noch \(n / 2^i\) Elemente in der Liste.
Ergo ergibt sich ein Aufwand von \(O(n log(n))\). Das trifft die untere Schranke für das vergleichsbasierte Sortieren.

1.3.6. Two-Phase, Multiway Merge-Sort (TPMMS)

TPMMS wird in vielen DBMS eingesetzt. Es besteht aus zwei Phasen:

Phase 1
In der ersten Phase werden jeweils so viele Tupel geladen wie in den Hauptspeicher passen. Die Teilstücke werden im Hauptspeicher sortiert und auf die Festplatte zurückgeschrieben. Das Ergebnis sind viele sortierte Teillisten auf der Festplatte.

Phase 2
In der Phase werden alle sortierten Teillisten zu einer einzigen großen Liste gemerged.

1.3.7. TPMMS - Phase 1

Der Rekursionsanfang ist nun nicht nur mit einem oder zwei Elementen! Die Sortierung der Teillisten erfolgt bei TPMMS z.B. mit Quicksort, welches im worst-case sehr selten ein Aufwand von O(n^2) hat.

Der Ablauf der ersten Phase hat drei Schritte:

1. Zunächst wird der verfügbare Hauptspeicher mit Diskblöcken aus der Originalrelation gefüllt

2. Die Tupel, die sich im Hauptspeicher befinden, werden sortiert.

3. Die sortierten Tupel werden auf die neuen Blöcke der Disk geschrieben. Das Ergebnis ist eine sortierte Teilliste.

Ein Beispiel dazu: Seien 6,400 Blöcke im Hauptspeicher; also insgesamt 100,000 Blöcke. Es sind 16 Füllungen des Hauptspeichers erforderlich. Die letzte Füllung ist kleiner.
Ein Aufwand von 200,000 I/O-Operationen ergibt sich, da 100,000 Blöcke gelesen und 100,000 Blöcke geschreiben werden.

Für eine I/O-Operation wird durchschnittlich eine Zeit von 11 ms benötigt. Insgesamt ergben sich \(11 ms · 200,000 = 2,200 s = 37 min\). Die Prozessorzeit für das Sortieren ist dabei vernachlässigbar.

1.3.8. TPMMS - Phase 2

Die naive Idee von Phase 2 ist das paarweise Mergen von k sortierten Teillisten. Man muss \(2 · log2(k)\) jeden Block (jedes Tupels) Lesen und Schreiben.

Im Beispiel: Ein Durchlauf für 16 sortierte Teillisten, einer für 8, einer für 4 und ein letzter für 2 sortierte Teillisten. Insgesamt ist jeder Block an 8 I/O-Operationen beteiligt. Es wird deutlich mehr Zeit benötigt. Eine bessere Idee wäre es nur den ersten Block jeder Teilliste zu lesen:

1. Suche den kleinsten Schlüssel unter den ersten Tupeln aller Blöcke (Lineare Suche (lin.), Priority Queue (log.)).

2. Bewege dieses Element in den Output-Block (im Hauptspeicher).

3. Falls der Output-Block voll ist, schreibe ihn auf die Festplatte.

4. Falls ein Input-Block leer ist, lese den nächsten Block aus derselben Liste. Der Aufwand beträgt 2 I/O-Operationen pro Block (und Tupel). Dies dauert ebenfalls 37 Minuten.

Die Laufzeit für TPMMS insgesamt beträgt somit 74 Minuten.

1.3.9. Bemerkungen zur Blockgröße

Es lässt sich beobachten, dass je größer die Blockgröße ist, desto weniger I/O-Operationen werden benötigt. Die Transferzeit erhöht sich dabei etwas.

Das bisherige Beispiel:

• Blockgröße: 16 KB

• ∅ Latenzzeit: 10,88 ms (davon nur 0,253 ms für Transfer)

Das neue Beispiel mit erhöhter Blockgröße:

• Blockgröße: 512 KB (16 · 32)

• ∅ Latenzzeit: 20 ms (davon 8 ms für Transfer)

Es werden nur noch 12.500 I/O-Operationen für die Sortierung benötigt. Die Gesamtzeit beträgt 4,16 Minuten. Es ergibt sich eine 17-fache Beschleunigung!

Die Nachteile der Blockvergrößerung:

- Blocks sollten sich nicht über mehrere Spuren erstrecken.
- Kleine Relationen nutzen nur Bruchteile eines Blocks, was zu Speicherverschwendung führt.
- Viele Datenstrukturen für Externspeicher bevorzugen die Aufteilung von Daten auf viele kleine Blöcke.

1.3.10. TPMMS – Grenzen

Vorweg ein paar Stichpunkte zur Notation:

• Blockgröße: B Bytes

• Hauptspeichergröße (für Blocks): M Bytes

• Tupelgröße: R Bytes
  

Grenzen:

• Man kann somit sagen, dass \(\frac {M}{B}\) Blöcke in den Hauptspeicher passen.

• In Phase 2 wird außerdem Platz für einen Outputblock benötigt.

• Phase 1 kann also genau \(\frac{M}{B}- 1\) sortierte Teillisten erzeugen. Ebenso oft kann der Hauptspeicher mit Tupeln gefüllt und sortiert werden (in Phase 1). Jede Füllung enthält \(\frac {M}{R}\) Tupel.

• Maximal können \((\frac{M}{R}) \cdot ((\frac{M}{B}) - 1)\) Tupel sortiert werden.
  
  

• In dem Beispiel:

  • M = 104,857,600 Bytes

  • B = 16,384 Bytes

  • R = 160 Bytes

  • Zusammen ergibt sich eine maximale Eingabegröße von 4.2 Milliarden Tupeln (ca. 0.67 Terabyte)

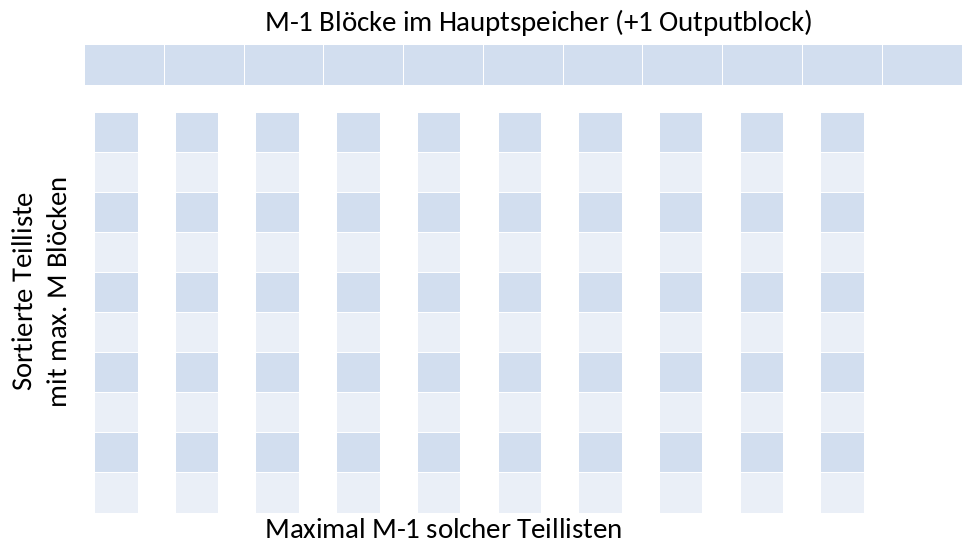
Fig. 1.21 TPMMS Grenzen Visualisierung

Falls die Eingaberelation noch größer ist, wird eine dritte Phase hinzugefügt. TPMMS wird genutzt, um sortierte Listen der Größe \(\frac {M^2}{RB}\) zu erzeugen. In der dritten Phase wird maximal \(\frac {M}{B} - 1\) solcher Listen zu einer sortierten Liste zusammengemerged. Insgesamt sind \(\frac{M^3}{RB^2}\) Tupel sortierbar. Bezogen auf unser Beispiel, gibt es nun eine maximale Eingabegröße von 27 Billionen Tupeln (ca. 4.3 Petabytes). Global betrachtet ist die zweite Phase die zusätzliche Phase.

1.4. Zugriffsbeschleunigung

Bisher waren die Annahmen, dass es nur eine Disk gibt und die Blockzugriffe (viele kleine Anfragen) zufällig geschehen. Dafür gibt es verschiedene Verbesserungsideen:

• Blöcke, die gemeinsam gelesen werden, werden auf dem gleichen Zylinder platziert, um die Suchzeit zu reduzieren.

• Die Daten werden auf mehrere (kleine) Disks verteilt (Verteilung), sodass man unabhängige Schreib-/Leseköpfe hat, die es ermöglichen mehrere (unabhängige) Blockzugriffe gleichzeitig durchzuführen.

• Spiegelung von Daten auf mehrere Disks.

• Verwendung eines Disk-Scheduling-Algorithmus.

• Prefetching von Blöcken: Das Ablegen von Blöcken im Hauptspeicher, die möglicherweise demnächst benötigt werden.

1.4.1. Daten gemäß Zylinder organisieren

Die Seektime macht ca. 50% der durchschnittlichen Blockzugriffszeit aus. Beim Megatron 747 beträgt die Seektime zwischen 0 und 40 ms. Die Idee dabei ist es die Daten, die zusammen gelesen werden, auf dem gleichen Zylinder zu platzieren. Zum Beispiel die Tupel einer Relation. Falls ein Zylinder nicht ausreicht, werden mehrere nebeneinander liegende Zylinder genutzt. Beim Lesen einer Relation fällt im besten Fall nur einmal die Seektime und Rotationslatenz an. Es wird nun die minimale Zugriffszeit der Disk erreicht: Die Zugriffszeit wird nur noch durch die Transferzeit bestimmt.
Ein Zylinder der Megatron 747 fasst 16 · 64 = 1024 Blöcke. Dennoch sind dann 16 Umdrehungen erforderlich (+ 15x seek über je eine Spur).

1.4.2. Zylinderorganisation - Beispiel

Ein paar Daten zur Megatron 747-Festplatte:

• Mittlere Transferzeit pro Block: ¼ ms.

• Mittlere seek time: 6,46 ms

• Mittlere Rotationslatenzzeit: 4,17 ms

• 16 Oberflächen mit 65.536 Spuren á 64 Blöcke (durchschnittlich)

Die Sortierung von 10 Mio. Tupeln mittels des TPMMS-Algorithmus dauerte 74 min. 100.000 Blöcke von R belegen 1563 Spuren (98 Zylinder).

Im ersten Teil der Phase 1 kommt es zum Lesen der Blöcke. Dazu wird der Hauptspeicher (mit 6400 Blöcke) 16 mal gefüllt. Es müssen die Blöcke von 6400/1024 = 6-7 Zylindern gelesen werden, die aber direkt nebeneinander liegen. Der Spurwechsel kostet nur 1ms. Die Reihenfolge beim Lesen der Tupel ist egal, wodurch man sich Rotationslatenzzeit spart. Die Zeit pro Füllung ergibt sich durch: - 6,46 ms + 6 ms + 6x8ms + 1,6s ≈ 1,6 s - Also: (1.seek) + (ca. 6 Spurwechsel) + (6 Rotationen) + (Transfer 6400 Blöcke) - Insgesamt: 1,6s x 16 Füllungen = 26s (<<18min)

Im zweiten Teil der Phase 1 kommt es zum Schreiben: analog zum Lesen ergibt sich beim Schreiben zusammen 52s. Vorher waren es 37 min. Achtung dabei: Die Rotationslatenz ist hier eigentlich wieder relevant…

Phase 2 wird nicht beschleunigt. Es wird aus verschiedenen (verteilten) Teillisten gelesen. Das Schreiben des Ausgabepuffers ist zwar sequentiell, wird aber von Leseoperationen unterbrochen.

1.4.3. Mehrere Disks

Bei der Nutzung von einer Disk gibt es das Problem, dass sich die S-/L-Köpfe einer Festplatte stets gemeinsam bewegen. Als Lösung des Problems kann man mehrere Festplatten (mit unabhängigen Köpfen) nutzen unter der Annahme, dass Disk-Controller, Hauptspeicher und Bus mit höheren Transferraten klarkommen. Das Resultat aus der Nutzung mehrerer Festplatten ist die Division aller Zugriffszeiten durch die Festplattenanzahl.
Eine Megatron 737 hat im Gegensatz zur Megatron 747 nur 2 Platten (also 4 Plattenoberflächen). Im Vergleich dazu hat die Megatron 747 8 Platten (also 16 Plattenoberflächen). Dementsprechend soll nun eine Megatron 747 durch vier Megatron 737 ersetzt werden, um die Zugriffszeiten zu minimieren. R wird somit auf 4 Festplatten verteilt.

TPMMS - Phase 1

Von jeder Platte müssen nun nur ¼ der Daten (1600 Blöcke) gelesen (Lesen) werden. Durch die günstige Zylinderorganisation ist die Seektime und Rotationslatenz ungefähr 0. Die Transferzeit benötigt 600 Blöcke × 0,25 ms (mittlere Transferzeit)= 400 ms pro Füllung. Bei 16 Füllungen und 400 ms pro Füllung dauert dies insgesamt: 16 Füllungen x 400 ms = 6,4 s.

Beim Schreiben wird jede Teilliste auf 4 Disks verteilt. Dies benötigit so viel Zeit wie beim Lesen: 6,4 s. Zusammen also ungefähr 13s statt 52s zuvor bzw. 37 min bei zufälliger Anordnung.

TPMMS - Phase 2
In der zweiten Phase nützt die Verteilung auf 4 Disks zunächst nichts. Immer wenn ein Block einer Teilliste abgearbeitet ist, wird ein nächster Block dieser Teilliste in den Hauptspeicher geladen. Erst wenn der nächste Block vollständig geladen ist, kann das Mergen fortgesetzt werden.
Der Trick beim Lesen ist es, dass das Mergen fortgesetzt werden kann bevor der Block vollständig in den Hauptspeicher geladen wurde. Das erste Element genügt schon. So können potenziell mehrere Blöcke parallel (jeweils einer pro Teilliste) geladen werden. Dabei kommt es zu einer Verbesserung, sofern diese auf unterschiedlichen Festplatten sind. Man sollte Vorsicht walten lassen, da es eine sehr delikate Implementierung ist. Damit befassen sich unter Anderem Datenbank- oder auch Systemingenieure.
Beim Schreiben des Outputs werden mehrere Output-Blöcke (hier: 4) verwendet. Einer wird gefüllt während die anderen drei geschrieben werden oder parallel, wenn auf unterschiedliche Festplatten geschrieben wird.
Die geschätzte Beschleunigung von Phase 2 beträgt einen Faktor von 2 bis 3.

1.4.4. Disk Scheduling

Beim Disk Scheduling soll der Disk-Controller entscheiden, welche Zugriffsanweisungen zuerst ausgeführt werden. Das ist nützlich bei vielen kleinen Prozessen auf je wenigen Blöcken. Häufig somit der Fall bei OLTP (Online Transaction Processing). Dabei ist die Erhöhung des Durchsatzes das Ziel.
Elevator Algorithmus Die Idee des Algorithmus kommt von Fahrstühlen. Ein Fahrstuhl fährt in einem Gebäude hoch und runter und hält an Stockwerken an, wenn jemand ein- oder aussteigen will. Er dreht um, falls weiter oben/unten keiner mehr wartet.
Analog dazu streicht ein Diskkopf über die Oberfläche einwärts und auswärts und hält an Zylindern an, wenn es eine (oder mehrere) Zugriffsanweisung(en) gibt. Er dreht um, falls in der jeweiligen Richtung keine Anweisungen mehr ausstehen.

1.4.5. Spiegelung

Die Idee der Spiegelung ist es, dass zwei oder mehr Festplatten identische Kopien halten. Dadurch entsteht mehr Sicherheit vor Datenverlust und man hat einen beschleunigten Lesezugriff. Bei n Festplatten kann es bis zu n mal so schnell sein.
Beim Lesen in der 2. Phase von TPMMS klappt der Trick wie bei mehreren Disks nicht immer. Es gibt keine Verbesserung, falls Blöcke verschiedener Teillisten auf der gleichen Festplatte liegen. Bei einer Spiegelung kann garantiert werden, dass immer so viele Blöcke unterschiedlicher Teillisten parallel gefüllt werden, wie Spiegelungen vorhanden sind.
Ein weiterer Vorteil, auch ohne Parallelität bei weniger als n Blöcke gleichzeitig: Es ist möglich die Festplatte auszuwählen, auf die zugegriffen wird. Man sollte die Festplatte wählen, deren Kopf am dichtesten an der relevanten Spur steht.
Ein paar weitere Anmerkungen zu Spiegelungen: Sie sind teuer und verursachen keine Beschleunigung des Schreibzugriffs, aber auch keine Verlangsamung.

1.4.6. First-Come-First-Serve vs. Elevator Algorithmus

Das Beispiel in Abbildung 1.22 zeigt den Vergleich zwischen First Come First Serve (kurz FCFS) und dem Elevator Algorithmus. Der Elevator-Algorithmus ist hierbei mit 57,52 nur etwas schneller als FCFS mit 71,52. In größeren Beispielen ist der Unterschied ausgeprägter.

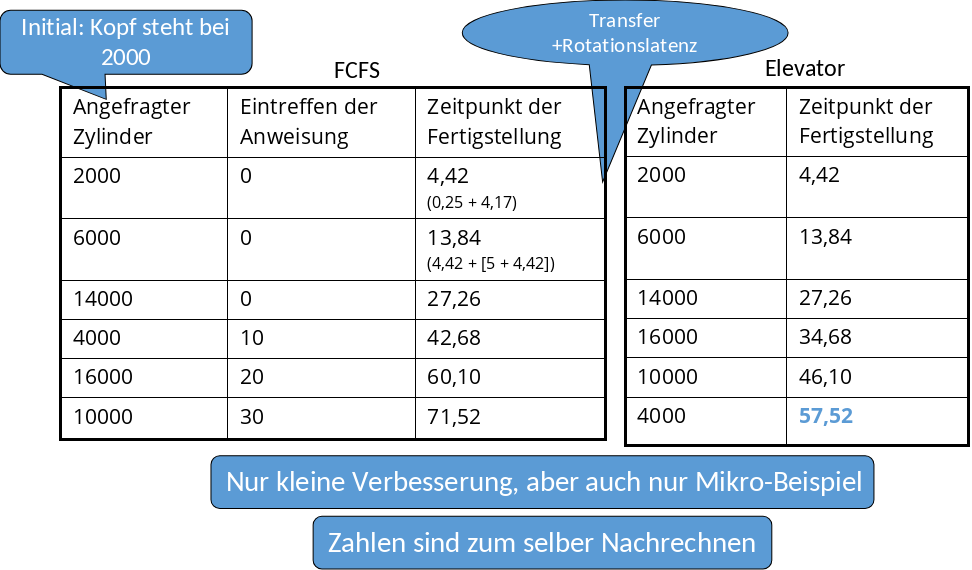
Fig. 1.22 FCFS vs. Elevator-Algorithmus

1.4.7. Elevator Algorithmus

Die Verbesserung durch den Elevator Algorithmus steigt mit durchschnittlicher Anzahl von wartenden Anweisungen. Bei so vielen wartenden Zugriffsanweisungen wie die Anzahl an Zylindern geht jeder Seek nur über wenige Zylinder. Die durchschnittliche Seektime (bezogen auf die wartenden Zugriffsanweisungen) wird verringert.
Grundsätzlich gibt es weniger Zylinder als es Zugriffsanweisungen gibt. Es gibt mehrere Zugriffsanweisungen pro Zylinder, die gleichzeitig verarbeitet werden können. Man kann zudem noch die Anweisungen sinnvoll sortieren, sodass man die Blöcke in sinnvoller Reihenfolge von den Zylindern liest. Dadurch reduziert sich die Rotationslatenzzeit.
Zu einem Nachteil kommt es, falls die Anzahl wartender Anweisungen zu groß ist. Die Wartezeiten für einzelne Zugriffsanweisungen werden dann sehr groß!

1.4.8. Prefetching

Die Idee von Prefetching ist es, voraussagen zu können, welche Blöcke in naher Zukunft gebraucht werden. Diese kann man dann früh (bzw. während man sie sowieso passiert) in den Hauptspeicher laden.
Beim Lesen in der 2. Phase von TPMMS werden 16 Blöcke für die 16 Teillisten reserviert. Es ist viel Hauptspeicher frei. Daher können zwei Blöcke pro Teilliste reserviert werden. Man geht bei TPMMS sowieso davon aus, dass der nächste Block irgendwann gelesen wird. Ein Block wird dann gefüllt, während der andere abgearbeitet wird. Wenn einer entleert ist, wird zum Anderen gewechselt. Die Laufzeit wird aber nicht verbessert.
Daher als Idee zur Verbesserung: Die Kombination mit guter Spur- oder Zylinderorganisation. Beim Schreiben in Phase 1 von TPMMS sollen Teillisten auf ganze, aufeinanderfolgende Spuren / Zylinder geschrieben werden. Beim Lesen in Phase 2 von TPMMS sollen ganze Spuren / Zylinder gelesen werden, wenn aus einer Liste ein neuer Block benötigt wird.
Die Idee für das Schreiben ist analog. Nicht jeder Block, der fertig ist, soll direkt auf die Disk geschrieben werden. Die Schreiboperationen sollen hinausgezögert werden bis die ganze Spur / der ganze Zylinder geschrieben werden kann. Außerdem sollen mehrere Ausgabepuffer verwendet werden. Während einer auf die Festplatte geleert wird, wird in den Anderen geschrieben.