Anfrageausführung

4. Anfrageausführung#

Zoom in die interne Ebene

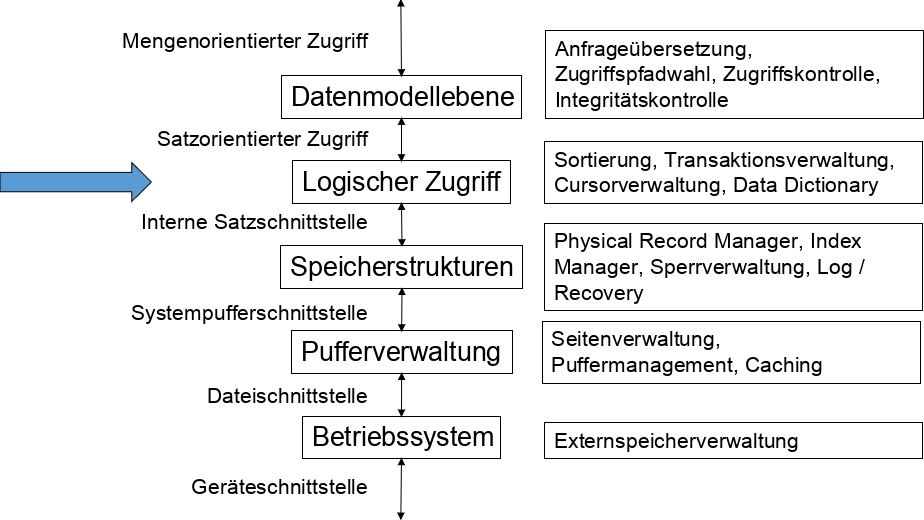
../_images/5-Schichten-Architektur2.png — Fig. 4.1 5-Schichten Architektur#

In den vorherigen Kapiteln haben wir die Anfragesprache bereits kennengelernt. Wir wissen jetzt, wie man Anfragen formulieren kann, wie Daten auf der Festplatte gespeichert werden und wie man den Zugriff auf die Daten mit Indizes beschleunigt.

Jetzt ist die Frage: Wie kommt man von der Anfrage bis zur Ausführung?

Zunächst haben wir eine SQL-Anfrage. Diese wird geparsed und daraus entsteht ein Parsebaum der prüft, ob diese Anfrage korrekt ist. Der Parsebaum wird dann in einen logischen Anfrageplan umgewandelt, der durch die Abschätzung der Kardinalitäten zeigt, wie eine logische Ausführung aussehen würde. Man versucht so die Operationen und ihre Reihenfolge auf logischer Ebene zu optimieren. Dann werden physische Pläne entworfen und man schaut, welche konkreten Implementierungen für einen bestimmten Operator Sinn machen würden. Für jeden Operator gibt es verschiedene Implementierungen, den Join Operator kann man beispielsweise als Loop Join oder auch Hash Join implementieren. Im nächsten Schritt werden die Pläne noch einmal begutachtet und die Kosten ein weiteres Mal geschätzt, damit der beste Plan ausgewählt werden kann. Führt man diesen dann aus, gibt es ein Anfrageergebnis zurück. Da man die Kardinalitäten nur abschätzt, hat man nicht die genauen Zahlen. Bei der Ausführung der Anfrage sieht man dann, wie lange diese tatsächlich braucht, ob sie vielleicht länger gebraucht hat, als erwartet, oder ob die Ausgabemenge sogar viel größer ist als geschätzt.

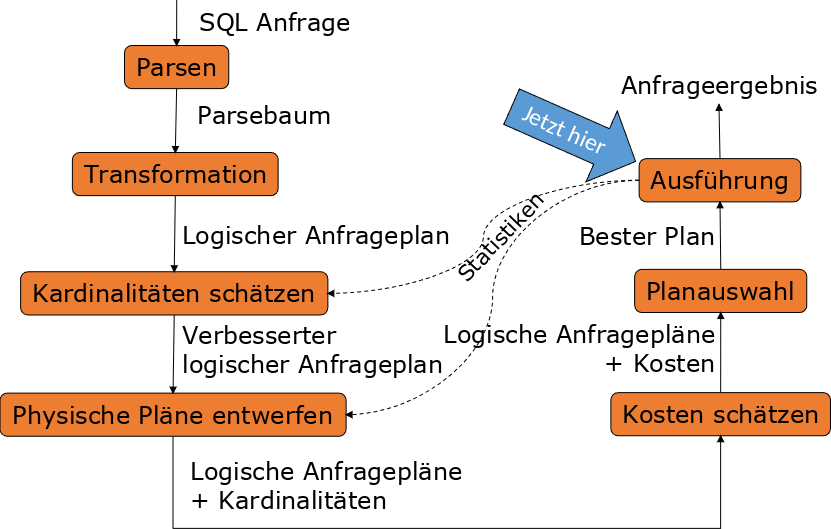
../_images/Ablauf-Anfragenbearbeitung.png — Fig. 4.2 Ablauf der Anfragenbearbeitung - die Ausführung#

Mit diesem Kapitel befinden wir uns in der Anfrageausführung und schauen uns konkret an, wie Operatoren umgesetzt werden.

4.1. Physische Operatoren#

Anfragepläne bestehen aus Operatoren. Bevor wir Kosten schätzen können müssen wir diese Operatoren kennen. Wir kennen bereits die Operatoren der Relationalen Algebra, welche auf physische Operatoren abgebildet werden. Was jetzt als neuer Operator dazu kommt, ist die Art und Weise, wie man eine Tabelle scannt.
Für jeden logischen Operator hat man mindestens einen physischen Operator der diesen implementiert. Später können noch Varianten von logischen Operatoren hinzukommen. Ein Join lässt sich beispielsweise unterschiedlich ausführen.

4.1.1. Tabellen Scannen#

Eine Tabelle zu scannen ist die einfachste Operation. Dabei wird die gesamte Relation eingelesen, was unter anderem bei Joins und Unions erforderlich ist. Den Scan kann man ggf. auch anpassen, indem man diesen mit Selektionsbedingungen kombiniert, um zum Beispiel nur die Blöcke zu suchen, die einen bestimmten Wert enthalten.

Es gibt zwei Scan Varianten, den Table-scan und den Index-scan. Beim Table-scan, werden alle Blöcke eingelesen, die in einer (bekannten) Region der Festplatte liegen. Dies bietet sich an, wenn man alle Operationen lesen will und die Tupelreihenfolge keine Rolle spielt.

Beim Index-scan gibt es einen Index, der angibt, welche Blöcke zur Relation gehören und wo diese liegen. Hat man eine Selektionsbedingung bietet sich der Index-scan hier am ehesten an, da wir direkt zu den bestimmten Werten springen können. Dieser steht außerdem stellvertretend für u.a. den B-Baum Index und den Hash Index.

4.1.2. Sortiertes Einlesen#

Eine weitere besondere Variante des Scans ist der Sort-scan - das sortierte Einlesen. Dies ist nützlich, wenn man in der Anfrage mit Order By sortiert oder wenn man bestimmte Operation, wie zum Beispiel Bereichsanfragen, ausführen will. Dann kann man mit Sort-scan, basierend auf einem gegeben Sortierschüssel, welcher aus einem oder mehreren Attributen und einer Sortierreihenfolge besteht, die Relation sortiert zurückgeben.

Es gibt unterschiedliche Implementierungsvarianten. Man kann zum Beispiel einen B-Baum haben der einen Sortierschlüssel als Suchschlüssel hat oder eine sequentielle Datei, die nach einem Sortierschlüssel sortiert ist. Ist die Relation klein kann diese im Hauptspeicher sortiert werden. Dann nutzt man entweder den Table-scan oder den Index-scan plus eine Sortierung. Ist die Relation hingegen sehr groß, muss man den TPMMS durchführen. Damit ist die Ausgabe nicht auf der Festplatte sondern als Iterator im Ausführungsplan.

4.1.3. Berechnungsmodell#

Bei der Ermittlung der Kosten eines Operators werden nur die I/O-Kosten berechnet, da diese die CPU-Kosten dominieren. Nehmen wir an, der Input eines Operators wird von der Disk gelesen, während der Output nicht auf die Disk geschrieben werden muss. Handelt es sich bei dem Operator um den letzten im Baum, verarbeitet die Anwendung die Tupel einzeln. Die I/O-Kosten hängen in diesem Fall von der Anfrage ab, nicht vom Plan. Handelt es sich aber um einen inneren Operator, kann man Pipelining durchführen, d.h. ein Tupel wird gelesen, zum nächsten Operator gegeben und immer so weiter. Damit hat man immer dieselben I/O-Kosten verbraucht, da das Tupel wie am Fließband von Operator zu Operator gereicht wird.

4.1.4. Kostenparameter / Statistiken#

Der verfügbare Hauptspeicher für einen Operator beträgt \(M\) Einheiten. Eine Einheit ist eine Blockgröße die wir auf der Festplatte haben. Den Hauptspeicherverbrauch messen wir nur für den Input der Operatoren, nicht für den Output. Wie viel Hauptspeicher man braucht, kann man dynamisch während der Anfragebearbeitung bestimmen. Wir gehen davon aus, dass \(M\) eine Schätzung ist und die Kosten, die wir schätzen können, nie genau sind. Der gewählte Plan, den wir als besten Plan ausgeben, ist somit nicht unbedingt auch der beste Plan. Basierend auf den Schätzungen ist es der Beste, dieser kann aber auch suboptimal sein.

\(B\) ist die Anzahl der Blöcke, \(B(R)\) ist die Anzahl aller Blöcke der Relation. Wir nehmen sogar an, dass \(B(R)\) die Anzahl der tatsächlich belegten Blöcke ist.

\(T\) ist die Anzahl der Tupel, \(T(R)\) ist die Anzahl der Tupel einer Relation. Mit \(\frac{T}{B}\) können wir die ungefähre Anzahl der Tupel pro Block berechnen.

\(V\) ist die Anzahl unterschiedlicher Werte (DISTINCT values) , d.h. die Kardinalität jeder Spalte. \(V(R,a)\) ist die Anzahl unterschiedlicher Werte einer Relation \(R\) im Attribut \(a\).

\(V(R, [a1,a2,…,an]) = |\delta(\pi_{a1,a2,…,an}(R))|\) –> Betrag der Duplikatentfernung = Anzahl unterschiedlicher Werte

Scan-Kosten Beispiele

Nun gibt es zusätzlich noch zu berücksichtigen, ob eine Relation geclustered ist oder nicht. Ist \(R\) clustered gespeichert, liegen alle relevanten Tupel nebeneinander. Bei einem Table-scan werden alle Blöcke gelesen, also betragen die Kosten \(B(R)\). Wenn sortiert werden soll und \(R\) in den Hauptspeicher passt, betragen die Kosten für einen Sort-scan \(B\). Passt \(R\) nicht, müssen wir TPMMS anwenden und die Kosten betragen dann \(3B\).
Ist \(R\) nicht geclustered, also die Blöcke nicht nebeneinanderliegend, sondern gemischt mit Tupeln anderer Relationen, betragen die Kosten für einen Table-scan im schlimmsten Fall \(T(R)\). Soll wieder sortiert werden, und \(R\) passt in den Hauptspeicher, liegen die Kosten für einen Sort-scan bei \(T\). Passt \(R\) aber nicht und wir müssen wieder TPMMS anwenden, betragen die Kosten \(T+2B\).

Die Kosten für einen Index-scan sind \(B\) oder \(T\). Ist der Index selbst einige Blöcke groß, handelt es sich meistens um kleinere Zahlen. Bei einem Baum beispielsweise rechnet man plus die Höhe, denn je nach dem was schon im Hauptspeicher liegt, ob es die Wurzel ist oder mehrere Ebenen, hat man mehr I/O-Operationen.

4.1.5. Iteratoren#

Viele physische Operatoren werden als Iterator implementiert. Für jede Operation haben wir drei bestimmte Grundfunktionen: Open(), GetNext() und Close().
Die Open-Funktion initialisiert Datenstrukturen und öffnet einen Iterator für eine Operation. Diese kann zum Beispiel ein Scan sein oder auch ein Join und diese Operation ruft dann die Open-Funktionen für alle anderen Operationen auf, die im Baum darunter liegen. Auf jeder Ebene des Baumes wird Open() aufgerufen. Die Funktion holt aber noch keine Tupel nach oben.

Mit der GetNext-Funktion holt man das nächste Tupel. Wendet man die Funktion auf den obersten Iterator an, ruft dieser wiederrum GetNext() für die Iteratoren darunter auf und geht dabei so tief wie nötig. Ist kein Tupel mehr vorhanden, bekommt man ein NotFound zurück.

Close() beendet und schließt den Iterator und ruft Close() auch für die anderen Iteratoren auf.

Pull-basierte Anfrageauswertung

In der Abbildung 4.3 lässt sich gut erkennen, wie Open() und GetNext() funktionieren. Wird in dem obersten Iterator Open() aufgerufen, wird auch in allen darunterliegenden Iteratoren Open() aufgerufen. R1-R4 symbolisieren die Scan Operationen. Mit GetNext() geht man die Iteratoren durch, bis ganz nach unten und holt dann das Ergebnis nach oben.

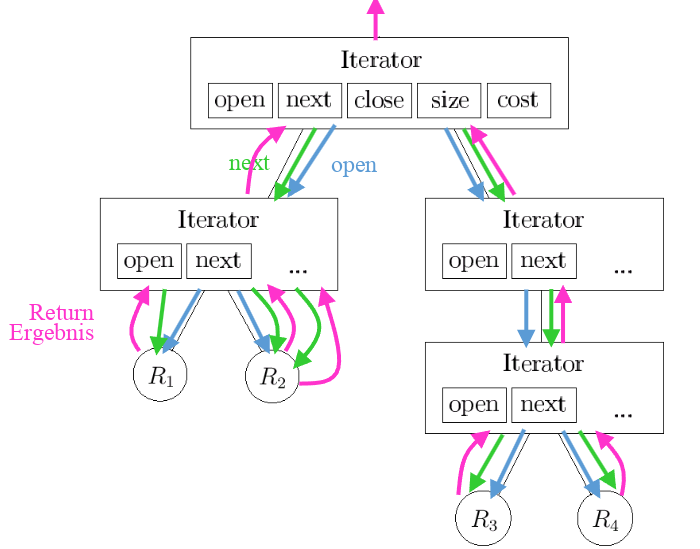
../_images/Pull-basierte-Anfragenauswertung.png — Fig. 4.3 Iterator Beispiel#

Iterator Beispiel - Table-scan

Im folgenden sehen wir einen Table scan:

Wir können einen Parameter \(b\) auf den ersten Block aus \(R\) setzen oder auf das erste Tupel.

Open()
    b := the first block of R;
    t := the first tuple of block b; 

Falls \(t\) das letzte Tupel war, gehen wir zum nächsten Block. Gibt es keinen weiteren Block, wird NotFound ausgegeben. Andernfalls gibt uns die Funktion das erste Tupel dieses Blocks aus und setzt den Zeiger dann auf das nächste Tupel.

GetNext()
    IF (t is past the last tuple on block b)
    Increment b to the next block;
    IF (there is no next block)
        RETURN NotFound;
    ELSE
        t := the first tuple of block b;
    oldt := t;
    Increment t to the next tuple of b;
    RETURN oldt;

Close()
    Do Nothing

Iterator Beispiel - Union all

Das Beispiel zeigt ein Union all:

Open(R,S) {
    R.open();
    CurRel := R;
}

GetNext(R,S) {
    IF (CurRel = R) {
        t := R.GetNext();
        IF(t <> NotFound) /*R ist nicht erschöpft*/
            RETURN t;
        ELSE /*R ist erschöpft*/ {
            S.Open();
            CurRel := S;
        }
    }
    RETURN S.GetNext();
}


Close(R,S) {
    R.Close();
    S.Close()
}

In der Open-Funktion werden die beiden Relationen \(R\) und \(S\) geöffnet, angefangen mit \(R\). Außerdem wird die Variable CurRel mit der aktuellen Relation initialisiert.

Die GetNext()-Funktion führen wir dann auf das nächste Argument der Relation aus. Wird kein NotFound ausgegeben, geben wir das Tupel aus, andernfalls öffnen wir \(S\) und initialisieren CurRel mit \(S\). Danach führen wir S.GetNext() aus.

Iterator Beispiel - Blocking

In diesem Iterator Beispiel (siehe Fig. 4.4) sieht man unten die beiden Relationen StarsIn und MovieStar. Aus der Relation MovieStar werden mithilfe einer Selektion und einer Projektion alle Namen der Filmstars, die 1960 geboren wurden, herausprojiziert. StarsIn und MovieStar werden dann gejoint, um die Titel der Filme zu bekommen, in denen nur Schauspieler gespielt haben, die 1960 geboren wurden.

../_images/Iterator-Beispiel.png — Fig. 4.4 Iterator Beispiel zum Blocking#

Hier der Code zu diesem Beispiel:

p = projection.Open();
while (t <> NotFound)
    t = p.GetNext()
    return t;
p.Close();

Class projection {

    Open() {
        j = join.Open();
        while (t <> NotFound)
            t:=j.GetNext()
            tmp[i++]=t.title;
        j.Close();
    }

    GetNext( ) {
        if (cnt < tmp.size())
            return tmp[cnt++];
        else return NotFound;
    }

    Close() {
        discard(tmp);
    }
} 

Class join {

    Open() {
        l = table.open();
        while (tl <> NotFound)
            t1 = l.GetNext();
            r = projection.Open();
            while (tr <> NotFound)
                tr = r.GetNext();
                if tl.starname=tr.name
                    tmp[i++]=tl⋈tr;
            end while;
            l.Close();
        end while;
        r.Close();
    }

    GetNext( ) {
        if (cnt < tmp.size())
            return tmp[cnt++];
        else return NotFound;
    }

    Close() {
        discard(tmp);
    }
} 

Mit p = projection.open() starten wir die Projektion. Solange das Tupel nicht gefunden wurde, holen wir mit t = p.GetNext() das nächste Tupel aus der Projektion und schließen diese mit p.Close().

Die Implementierung der Open()-Funktion in der projection Klasse lädt alle Tupel in den Hauptspeicher. Mit der GetNext()-Funktion bedienen wir uns nur noch an diesen Tupel. Wir können also nicht mit GetNext() weiter machen bevor mit Open() nicht alles geladen wurde. Dieser Vorgang nennt sich Blocking.

Mit der Zeile j = join.Open() wird dann Open() in der join Klasse aufgerufen. Hier wird für jedes Tupel, dass mit der äußeren while-Schleife aus der linken Tabelle genommen wird, mit der inneren while-Schleife ein Tupel aus der rechten Tabelle gelesen.

Auch hier blockiert die Open()-Funktion und lädt die ganzen Tupel in den Hauptspeicher, sodass wir uns mit GetNext() wieder einfach nur daran bedienen müssen.

Pipelining vs. Pipeline-Breaker

Wir sehen hier die Relationen \(R\), \(S\) und \(T\). Die schwarzen Punkte sind die Tupel, die sich nach oben bewegen. Es gibt die Möglichkeit, Operatoren zu pipelinen. Das bedeutet, dass wir mit GetNext() jedes Tupel direkt aus der untersten Schicht holen können (siehe Fig. 4.5). Wenn aber irgendwo ein GetNext() in einem Open() enthalten ist, gibt es einen Blocker, in dem zunächst alle Tupel gesammelt werden. Dann spricht man von einem Pipeline-Breaker (siehe Fig. 4.6).

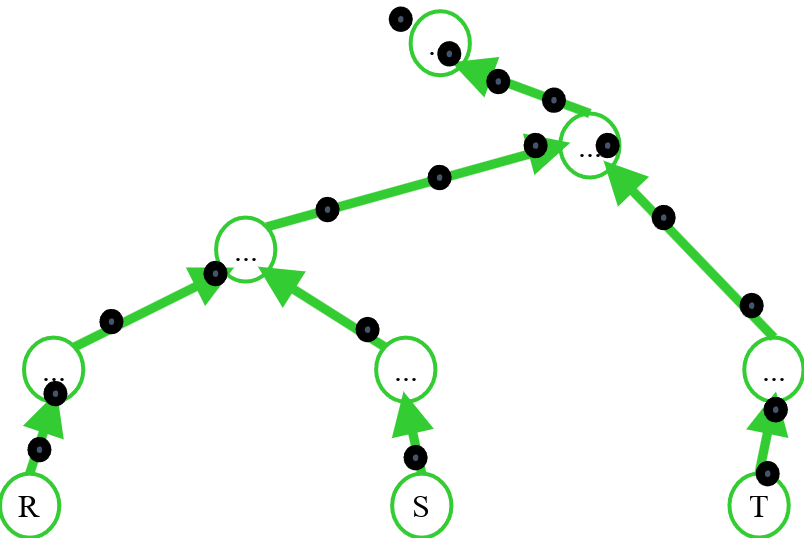
../_images/Pipelining-vs-Pipelin-Breaker_2.png — Fig. 4.5 Pipelining ohne Blocker#

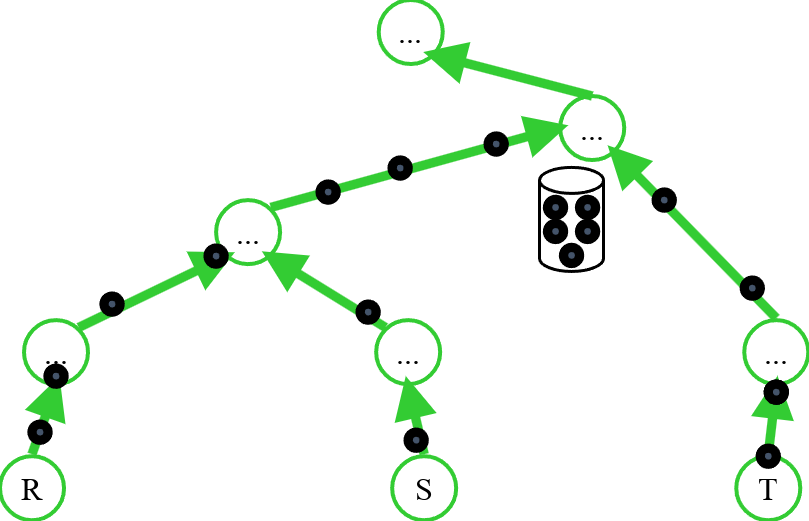
../_images/Pipelining-vs-Pipelin-Breaker.png — Fig. 4.6 Pipelining mit Pipeline-Breaker#

Pipelining versus Blocking

Pipelining ist im allgemeinen sehr vorteilhaft. Es müssen keine Zwischenergebnisse gespeichert werden und Operationen können auf Threads und CPUs verteilt werden. Wenn aber die gesamte Relation gelesen werden muss, braucht man Pipeline-Breaker. Das ist beispielsweise beim Sortieren der Fall. Hierbei muss die gesamte Relation gelesen werden, andernfalls kann next() nicht ausgeführt werden. Man unterbricht also die Verarbeitung der Daten in der Pipeline, um diese zu sortieren. Ist eine Relation sortiert oder gehashed kann next() diese auch gruppieren und aggregieren.

Union und Projektionen mit Duplikateliminierung scheinen auf den ersten Blick wie Pipeline-Breaker zu sein, da unterbrochen werden muss um alle Tupel miteinander zu vergleichen. Das ist aber nicht zwingend der Fall, denn die beiden Operatoren können die Tupel die sie bekommen in der GetNext()-Funktion vermerken. Beim nächsten Aufruf kann dann geprüft werden, ob dieses Tupel schon einmal gesehen wurde. Eine Sortierung ist hierfür nicht notwendig, da next() die Ergebnisse schon früh weiterreichen kann. Die effizienteste Methode ist dies nicht, da man für das merken der Tupel einen großen Zwischenspeicher braucht.
Aber: Einen Zwischenspeicher braucht man nur manchmal, in den anderen Fällen muss man die Operationen blocken (Blocking).

Iterator Beispiel - Pipelining

Hier noch einmal das selbe Beispiel wie zuvor. Diesmal pipelinen wir.

../_images/Iterator-Beispiele_2.png — Fig. 4.7 Iterator Beispiel zum Pipelining#

p = projection.Open();
while (t <> NotFound)
    t = p.GetNext()
return t; § p.Close();

Class projection {

    Open() {
        j = join.Open();
    }

    GetNext() {
        t = j.GetNext();
        return t.title
    }

    Close() {
        j.Close();
    }
} 

Class join {
    Open() {
        l = table.Open();
        r = projection.Open()
        tl = l.GetNext();
    }

    GetNext() {
        repeat{
            tr = r.GetNext();
            if (tr = NotFound){
                r.close();
                tl = l.GetNext();
                if (tl = NotFound)
                    return NotFound;
                r.open();
                tr = r.GetNext();
            }
        }
        until(tl.starname=tr.name)
        return tl⋈tr;
    }
    
    Close() {
        l.Close();
        r.Close();
    }
} 

In der Open()-Funktion wird jetzt nur noch der join geöffnet und keine Tupel mehr geladen, wie es beim Blocking der Fall war. In der Klasse join öffnen wir mit Open() nur die Relationen und GetNext() schaut was gelesen werden kann und was nicht.

Überblick über das Weitere

Es gibt drei Klassen von Algorithmen: Sort-basierte, Hash-basierte und Index-basierte Algorithmen. Diese sind entweder One-Pass Algorithmen, Two-Pass Algorithmen oder Multipass Algorithmen und haben somit drei Schwierigkeitsgrade die sich darin unterscheiden, wie oft über die Daten gelesen wird.

Die einfachsten Operatoren erfordern, dass nur einmal über die Daten gelesen wird. Das ist meist bei einem Scan der Fall, deshalb würde man hier einen One-Pass Algorithmus verwenden. Hier passt mindestens ein Argument in den Hauptspeicher, Selektion und Projektion ausgenommen.

Two-Pass Algorithmen, wie zum Beispiel TPMMS, finden meist Anwendung, wenn es eine Größenbeschränkung für den Input gibt. Hierbei wir meist erst einmal gelesen, dann wird zwischengespeichert und dieses Zwischenergebnis wird dann noch einmal gelesen.

Hat man zu wenig Speicherplatz für den Two-Pass Algorithmus kann man den Multipass Algorithmus verwenden. Dieser ist eine rekursive Erweiterung des Two-Pass Algorithmus und unbeschränkt in der Inputgröße, dafür aber unter anderem abhängig vom Operator.

4.2. One-Pass Algorithmen#

4.2.1. Operatorklassen für One-pass Verfahren#

Wir gehen immer davon aus, dass die Operationen und der Input in den Speicher passen.
Hat man Tupel-basierte unäre Operatoren braucht man nur einen sehr kleinen Teil des Inputs gleichzeitig im Hauptspeicher. Meist wenn Projektionen, Selektionen oder Multimengen-Vereinigungen durchgeführt werden.

Relationen-basierte unäre Operatoren benötigen meist die gesamte Relation gleichzeitig im Hauptspeicher. Deshalb darf die Inputgröße die Hauptspeichergröße nicht überschreiten. Dies ist der Fall bei Gruppierungen, Duplikateliminierungen und Sortierungen.

Relationen-basierte binäre Operatoren benötigen mindestens eine gesamte Relation im Hauptspeicher. Außerdem braucht man dann noch ein wenig Speicher für ein Element aus einer anderen Relation. Das gilt für alle Mengenoperationen außer Multimengen-Vereinigungen, aber vor allem für den Join.

4.2.2. Tupel-basierte unäre Operatoren#

Für Selektionen und Projektionen verwendet man Tupel-basierte unäre Operatoren, denn diese sind unabhängig von der Hauptspeichergröße. Die Speicherkosten betragen nur eine Einheit, da man immer nur ein Tupel auf einmal liest. Die I/O-Kosten hängen wie beim Table-scan oder Index-scan davon ab, ob \(R\) geclustered ist oder nicht. Ist \(R\) geclustered, betragen die Kosten \(B\), ist \(R\) nicht geclustered betragen die Kosten \(T\). Falls es einen Suchschlüssel im Index gibt, sind die Kosten noch geringer.

../_images/Tupel-basierte-unäre-Operatoren.png — Fig. 4.8 Tupel-basierte unäre Operation#

4.2.3. Relationen-basierte unäre Operatoren#

Relationen-basierte unäre Operatoren verwendet man bei Duplikateliminierungen und Gruppierungen. Hier ist zu beachten, dass die ganze Relation in den Hauptspeicher passen muss. Um dies zu bewältigen und um den Hauptspeicher ein wenig zu entlasten, ist es sinnvoll, nur die “Repräsentanten” zu speichern. Für die Duplikateliminierung bedeutet das, nicht alle Attribute eines Tupels zu speichern, sondern nur die, die die Tupel voneinander unterscheiden. Bei der Gruppierung würde man nur Gruppierungsattribute und aggregierte Teilergebnisse speichern und nicht das gesamte Tupel. Mit diesem “Trick” können dann auch größere Relationen verarbeitet werden.

4.2.3.1. Duplikateliminierung#

Bei der Duplikateliminierung wird Tupel für Tupel eingelesen. Wurde das Tupel zuvor noch nicht gesehen, wird es einfach ausgegeben, andernfalls passiert nichts. Der Puffer merkt sich, welche Tupel schon einmal gesehen wurden. Da man Tupel sofort finden möchte, sollte man sich eine geeignete Datenstruktur überlegen. Hier bieten sich am besten Hashtabellen oder balancierte Binärbäume an. Bei der Wahl von \(M\), also wie groß der Speicher sein muss, rechnet man die Anzahl der duplizierten Tupel (alle DISTINCT Werte der Relation) geteilt durch die Anzahl der Tupel pro Block. Das Ergebnis muss dann kleiner sein als \(M\), damit man die Duplikateliminierung mit einem One-Pass Algorithmus durchführen kann.

Wahl von \(M\): \(B(\delta(R)) = \frac {V(R, [A1, … ,An])} {Tupel-pro-Block}\) ≤ \(M\)

../_images/Duplikateliminierung.png — Fig. 4.9 Duplikateliminierung#

4.2.3.2. Gruppierung#

Bei der Gruppierung wird ein Eintrag pro Gruppe im Hauptspeicher, bzw. ein Eintrag pro Gruppierungswert erzeugt. Dazu nimmt man noch kumulierte Werte für aggregierte Attribute, wie zum Beispiel MIN/MAX, COUNT oder SUM. AVG ist etwas schwieriger, da sich der Wert ändern kann. Hierfür muss man sich zusätzlich noch COUNT und SUM merken, damit man dann am Ende AVG berechnen kann.

Der Output ist ein Tupel pro Eintrag und wird erst nach dem letzten Input ausgegeben, denn erst dann kann man sicher sein, dass jede Gruppe vollständig betrachtet wurde. Da die Einträge selbst größer oder kleiner als das Tupel sein können, sind die Hauptspeicherkosten schwer abzuschätzen. Die Anzahl der Einträge ist aber höchstens so groß wie \(T\). Meistens wird sogar weniger Speicher verwendet, als man Blöcke hat.

4.2.4. Relationen-basierte binäre Operatoren#

Zu den Relationen-basierten binären Operatoren gehören alle mengenbasierten Operatoren sowie Join und das Kreuzprodukt. Bei den mengenbasierten Operationen müssen wir die Multimengenvereinigung ausschließen. Hier ist anzumerken, das Multimengensemantik immer mit einem B (“Bag”) abgekürzt ist und Mengensemantik mit einem S (“Set”).

Es wird angenommen, dass immer eine Relation in den Hauptspeicher passt. Je nachdem, welche Operation man durchführen möchte, muss hier wieder eine sinnvolle Datenstruktur gewählt werden. Sollte nur eine Relation in den Hauptspeicher passen, nimmt man hier die kleinere. Wir gehen davon aus, dass \(B(S)\) kleiner als \(B(R)\) ist und die Kosten somit ungefähr \(B(S) + 1\) betragen. Deshalb würde man hier \(B(S)\) wählen.

4.2.4.1. Vereinigung#

Führt man die Vereinigung von \(R\) und \(S\) in Multimengensemantik durch \((R \cup_{B} S)\), ist das Tupel-basiert möglich. Die I/O-Kosten betragen \(B(R) + B(S)\), da beide Relationen gelesen werden müssen und der Hauptspeicherbedarf genau 1 beträgt.

Bei der Vereinigung von \(R\) und \(S\) in der Mengensemantik \((R \cup_{S} S)\) werden erst alle Tupel aus \(S\) eingelesen. Über diese Tupel wird dann eine Datenstruktur aufgebaut (Schlüssel ist ein gesamtes Tupel). Diese eingelesenen Tupel werden dann alle ausgegeben und als nächstes wird \(R\) eingelesen. Bei jedem Tupel, dass es auch in \(S\) gibt, wird nichts gemacht, die anderen werden auch ausgegeben.

4.2.4.2. Schnittmenge#

Nimmt man die Schnittmenge von \(R\) und \(S\) \((R \cap_{S} S)\), ist der Ablauf ähnlich wie bei der Vereinigung in Mengensemantik. Nach dem Einlesen von \(S\) gibt man aber noch keine Tupel aus, da man noch nicht weiß, ob diese in der Schnittmenge enthalten sind. Liest man dann \(R\) ein, werden die Tupel, die auch in \(S\) vorkommen, ausgegeben, für die anderen wird nichts getan. Voraussetzung für die Schnittmenge ist, dass \(R\) und \(S\) Mengen sind.

Bei der Schnittmenge von \(R\) und \(S\) in der Multimengensemantik \((R\cap_{B}S)\) wird \(S\) eingelesen und für jedes Tupel ein COUNT-Wert gespeichert, damit man sehen kann, wie oft ein Tupel gelesen wurde. Dann wird \(R\) eingelesen. Kommt ein Tupel aus \(R\) in \(S\) vor und der COUNT-Wert ist größer als Null, wird dieses Tupel ausgegeben und der COUNT-Wert um eins reduziert. In allen anderen Fällen wird nichts getan.

4.2.4.3. Mengen-Differenz#

Die Mengen-Differenz ist nicht kommutativ, deshalb ist es wichtig, dass man die Relation, von der man etwas abziehen möchte, zuerst nimmt. Auch hier ist wieder vorausgesetzt, dass \(R\) und \(S\) Mengen sind. Für die beiden folgenden Beispiele wird angenommen, dass \(S\) kleiner als \(R\) ist.

Im ersten Schritt wird immer die kleinere Relation, hier \(S\), in eine effiziente Datenstruktur eingelesen. Der Schlüssel ist ein gesamtes Tupel.

Nimmt man \(R-_{S}S\) , liest man \(R\) ein und gibt jedes nicht in \(S\) vorkommende Tupel aus. Die anderen Tupel werden ignoriert.
Nimmt man \(S-_{S}R\), liest man \(R\) ein und löscht alle auch in \(S\) vorkommenden Tupel aus der Datenstruktur. Kommt ein Tupel nicht in \(S\) vor, wird nichts getan. Alle übrigen Tupel werden einfach ausgegeben.

4.2.4.4. Multimengen-Differenz#

Auch die Multimengendifferenz ist nicht kommutativ und auch hier ist es wichtig, die Relation, von der man etwas abziehen möchte, zuerst zu nehmen.
Nimmt man \(S-_{B}R\) in der Multimengensemantik, liest man auch hier zuerst \(S\) ein und speichert wieder für jedes Tupel einen COUNT-Wert. Dann wird wieder \(R\) eingelesen und geschaut, ob es in der Relation Tupel gibt die auch in \(S\) vorkommen. Falls ja, wird der COUNT-Wert verringert, falls nein, wird nichts getan. Die Tupel werden dem COUNT-Wert entsprechend oft ausgegeben.

Bei \(R-_{B}S\) wird für jedes Tupel in \(S\) ein COUNT-Wert c gespeichert, welcher c Gründe liefert, ein Tupel aus \(R\) nicht auszugeben. Wird dann \(R\) eingelesen und ein Tupel ist bereits vorhanden und COUNT ist größer als Null, wird COUNT verringert. Ist COUNT gleich Null oder das Tupel noch nicht vorhanden, wird es ausgegeben.

4.2.4.5. Kreuzprodukt#

Bei dem Kreuzprodukt von \(R\) und \(S\) \((R × S)\) wird \(S\) wieder zuerst in den Hauptspeicher eingelesen, hierbei ist die Datenstruktur egal. Wird dann \(R\) eingelesen, konkatenieren wir mit jedem Tupel aus \(S\) und geben das Ergebnis aus. Die Rechenzeit pro Tupel ist sehr lang und die Ausgabe dementsprechend groß.

4.2.4.6. Natural Join#

Beim Natural Join \(R(X,Y) ⋈ S(Y,Z)\) wird zuerst \(S\) in den Hauptspeicher eingelesen. \(Y\) ist hier unser Suchschlüssel - das Join Attribut. Dann wird \(R\) eingelesen und man sucht für jedes Tupel der Relation ein passendes Tupel aus \(S\) und gibt es aus. Die I/O-Kosten betragen \(B(S) + B(R)\). Es wird angenommen, dass \(B(S) <= M-1\) bzw. \(<= M\) ist.

Equi-join und Theta-join funktionieren analog.

4.3. Nested Loop Join#

Zuvor haben wir uns mit Algorithmen und Operatoren beschäftigt, bei denen es ausgereicht hat, eine Relation nur einmal einzulesen, da diese als Ganzes in den Hauptspeicher passte. Nun schauen wir uns Algorithmen an, bei denen nicht mehr davon ausgegangen werden kann, dass der Hauptspeicher ausreichend groß ist.

Der Nested-Loop-Join-Algorithmus ist ein operationsabhängiges Verfahren und ein 1.5-Pass Algorithmus. Die Idee ist, dass eine Relation nur einmal eingelesen wird und die andere Relation mehrfach. Dabei kann die Größe der beiden Relationen beliebig sein.

Man könnte hier eine Tupel-basierte, naive Variante des Algorithmus durchführen. Dafür holt man sich jeweils ein Tupel aus der Relation \(S\) und ein Tupel aus der Relation \(R\) und prüft, ob man diese verjoinen kann. Falls ja, wird das Ergebnis ausgegeben.

FOR EACH TUPLE s IN S DO
    FOR EACH TUPLE r IN R DO
        IF (r.Y = s.Y) THEN OUTPUT (r ⋈ s)

Die I/O-Kosten sind \(T(S) + T(S) · T(R)\), denn man muss jedes Tupel aus S herausfinden und dann für jedes dieser Tupel R-mal alle Tupel aus \(R\) lesen. Das lässt sich optimieren, indem man zum Beispiel einen Index für das Joinattribut in \(R\) hat oder die Tupel auf Blöcke verteilt.

4.3.1. Block-basierter NLJ#

Beim Block-basierten Nested Loop Join werden die Tupel nach Blöcken organisiert, was besondern sinnvoll für die innere Schleife ist. Wir versuchen den Hauptspeicher so gut es geht zu nutzen, indem wir ein \(R\)-Tupel nicht nur mit einem, sondern mit vielen \(S\)-Tupeln verjoinen. Idealerweise ist die äußere Schleife für die kleinere Relation (hier \(S\)), damit weniger Vergleiche gemacht werden müssen. Dennoch ist dies schwieriger als im One-Pass, da \(B(S)\) größer als \(M\) ist. Aus dem Grund brauchen wir auch hier eine effiziente Datenstruktur für \(S\) im Hauptspeicher.

Im folgenden Codebeispiel sehen wir, wie so ein Block-basierter Nested Loop Join aussieht. Wir holen uns einen chunk von Blöcken aus \(S\) und lesen die Blöcke in den Hauptspeicher. Dann organisieren wir die Tupel in effiziente Datenstrukturen, sodass wir die Join Attribute besser als Schlüssel darstellen können. In der nächsten Schleife holen wir dann jeweils einen Block aus \(R\) und lesen für jeden Block die Tupel aus. Es werden drei Schleifen benötigt. Die ersten beiden sind für das blockweise Vorgehen zuständig und die Dritte wird gebraucht, weil im Block selber die Tupel im Hauptspeicher noch einmal gelesen werden müssen.

FOR EACH chunk of M-1 blocks of S DO BEGIN
    read blocks into main memory;
    organize tuples into efficient data structure;
    FOR EACH block b of R DO BEGIN
        read b into main memory;
        FOR EACH tuple t of b DO BEGIN
            find tuples of S in main memory that join;
            output those joined tuples;
        END;
    END;
END;

Block-basierter NLJ – Kosten

Sagen wir, wir haben eine Relation \(R\) mit 1000 Blöcken \((B(R) = 1000)\), eine Relation \(S\) mit 500 Blöcken \((B(S) = 500)\) und 101 Einheiten Platz im Hauptspeicher \((M = 101)\). Damit können wir im Hauptspeicher jeweils 100 Blöcke abbilden und jeweils einen Block für \(R\) merken, vorausgesetzt es werden keine weiteren Einheiten benötigt. Nun muss die äußere Schleife fünf Mal durchlaufen werden (5 · 100 I/O-Operationen = 500 I/O-Operationen). Dazu kommen jeweils 1000 I/O-Operationen für \(R\), womit wir auf insgesamt 5.500 I/O-Operationen kommen.

Wäre R jetzt in der äußeren Schleife, würde diese Relation zuerst gelesen werden und die Schleife müsste 10 Mal durchlaufen werden (10 · 100 I/O-Operationen = 1000 I/O-Operationen). Dazu würden wieder pro Schleifendurchlauf jeweils 500 I/O-Operationen für \(S\) hinzukommen und ein Ergebnis von 6000 I/O-Operationen liefern. Wie man sieht, ist es also sinnvoller wenn die kleinere Relation außen ist.

In einem weiteren Beispiel haben wir \(B(S) = 100\) und \(B(R) = 1.000.000\). Ist die Relation \(R\) außen, muss die Schleife 10.000 Mal laufen und bei jedem Durchlauf kommen 100 I/O-Operationen für \(S\) hinzu, sodass man am Ende 2.000.000 I/O-Operationen hat. Ist \(S\) in diesem Szenario aber außen, muss die Schleife nur einmal durchlaufen werden und man hat am Ende 1.000.100 I/O-Operationen. Also auch hier wieder deutlich, dass es sinnvoller ist, die kleinere Relation außen zu haben.

Im folgenden einmal eine allgemeinere Berechnung. Mit der äußeren Schleife werden so viele Blöcke gelesen, wie in den Hauptspeicher passen. Also wird hierfür die Anzahl der Blöcke von \(S\) durch den Platz im Hauptspeicher geteilt. Das wird multipliziert mit \(M-1\) Blöcken von \(S\), addiert mit der Anzahl der Blöcke von \(R\), für die innere Schleife. Das Ergebnis ist nur eine Abschätzung. Die Formel sieht wie folgt aus:

\(\frac{B(S)}{M-1}(M-1+B(R)) = \frac{B(S)(M-1)}{M-1} - \frac{B(S)}{M-1} + \frac{B(S)B(R)}{M-1} \approx\frac {B(S)B(R)}{M}\)

4.3.2. Zusammenfassung bisheriger Algorithmen#

In Abbildung 4.10 sehen wir eine Übersicht darüber, wie viel Hauptspeicher die verschiedenen Operationen in den verschiedenen Varianten benötigen und wie viel I/O dabei verbraucht wird.

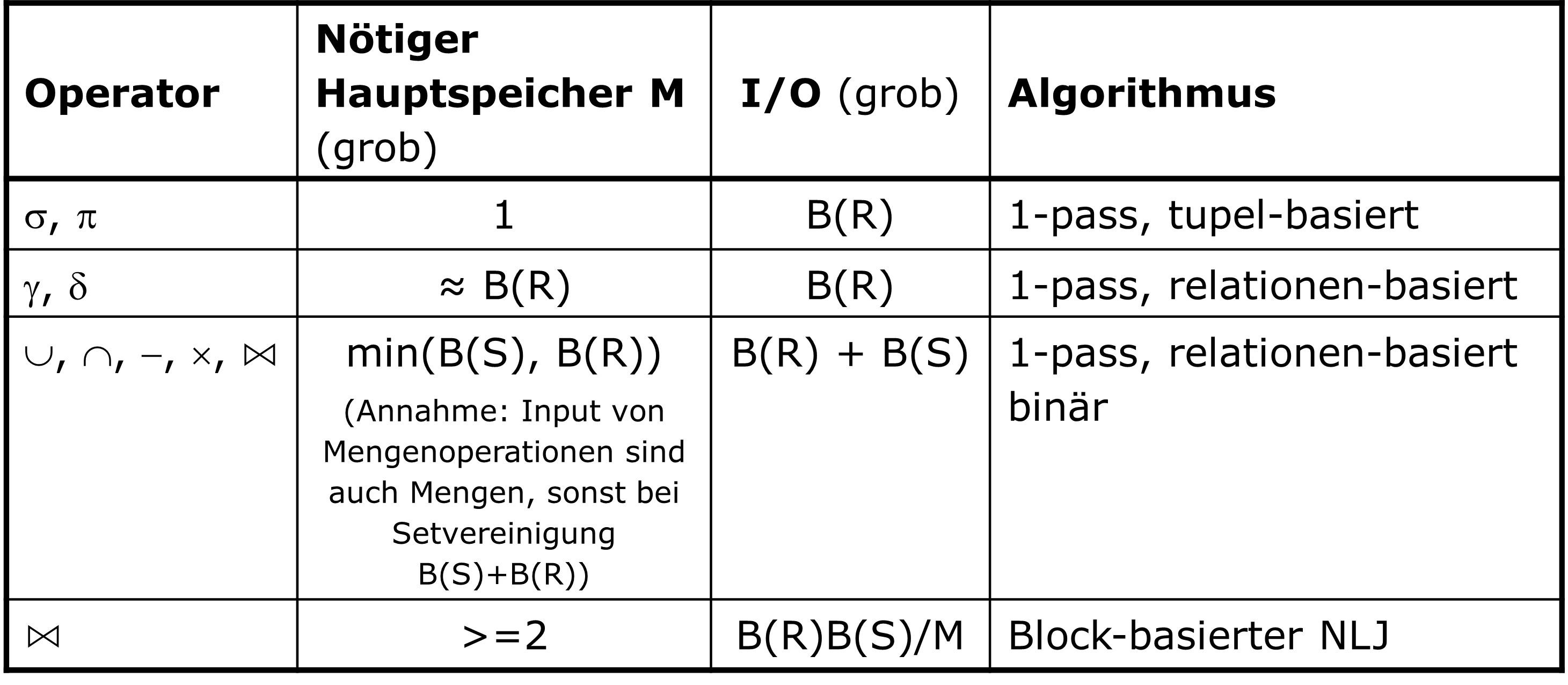
../_images/Zusammenfassung-Algorithmen.png — Fig. 4.10 Übersicht über die bisherigen Algorithmen#

4.4. Sort-basierte Two-Pass Algorithmen#

1-, 2-, Mehr-Phasen

Bisher haben wir uns mit One-Pass Algorithmen befasst, bei denen immer eine Relation in den Hauptspeicher passt. Nun befassen wir uns mit Two-Pass Algorithmen, bei denen mehrfach über eine Relation gelesen werden muss, weil diese nicht als ganzes in den Hauptspeicher passt. Es gibt eine, zwei oder auch mehrere Phasen, je nachdem wie groß die Liste ist, meist reichen aber zwei Phasen. Diese bestehen aus dem Einlesen der Daten, der Verarbeitung der Daten (z.B. eine Vorsortierung von Teillisten), dem Schreiben der Daten und dem Wiedereinlesen der Daten (z.B. Merging der Teillisten).

4.4.1. Duplikateliminierung#

Den ersten Algorithmus, den wir uns anschauen, ist die Duplikateliminierung. Hier ist das Vorgehen ähnlich wie bei TPMMS. In Phase 1 werden Teillisten erstellt, der Sortierschlüssel ist das gesamte Tupel. In der 2. Phase haben wir einen Block pro Teilliste und betrachten jeweils das erste Tupel. Hier suchen wir das kleinste Tupel und geben dieses aus. Alle anderen identischen Tupel werden verworfen.

Schauen wir uns das anhand eines Beispiels an. Nehmen wir an, wir haben im Hauptspeicher Platz für drei Blöcke und einen Outputblock \((M = 3 + 1)\). Es passen zwei Tupel in jeden Block und wir haben insgesamt 17 Tupel (2, 5, 2, 1, 2, 2, 4, 5, 4, 3, 4, 2, 1, 5, 2, 1, 3). In Phase 1 ergeben sich daraus drei sortierte Teillisten, denn wir müssen jeden Block vollständig füllen. Dabei können die Teillisten unterschiedliche Längen haben. In Phase 2 suchen wir uns dann immer das kleinste Tupel heraus und verschieben dieses in den Outputblock. Gleiche Tupel werden verworfen.

Dieser Algorithmus lässt sich noch optimieren, indem wir schon in Phase 1 die Duplikate in den Teillisten erliminieren. Damit lassen sich mehr Tupel in eine Teilliste laden und man hat kleinere Teillisten.

Duplikateliminierung Kosten

Die Kosten für die Duplikatelimierung liegen, wie beim TPMMS, bei \(3 · B(R)\). Jeweils das Einlesen der Daten, und das Schreiben und Lesen der Teillisten kostet \(B(R)\). Ist die Relation jedoch nicht geclustered, sind die Kosten für das Einlesen in Phase 1 \(T(R)\). In dem Fall würden wir insgesamt auf \(T(R) + 2 · B(R)\) kommen.

Die Kosten für den One-Pass Algorithmus liegen hingegen nur bei \(1 · B(R)\), da mit Two-Pass Algorithmen größerer Input möglich ist:

- One-pass: B ≤ M
- Two-pass: B ≤ M²

4.4.2. Gruppierung und Aggregation#

Die Gruppierung und Aggregation verläuft wieder sehr ähnlich. In Phase 1 lesen wir \(M\) Blöcke aus \(R\) ein und sortieren diese nach einem Gruppierungsattribut. Dann schreiben wir diese in sortierte Teillisten. In Phase 2 laden wir jeweils einen Block jeder Teilliste und suchen den kleinsten Schlüssel. Mit diesem Schlüssel aggregieren wir dann alle Tupel, ggf. müssen wir Blöcke nachladen. Am Ende geben wir ein Tupel mit den aggregierten Werten aus und suchen wieder den nächstkleineren Schlüssel. Die I/O-Kosten sind \(3 · B(R)\) und damit genauso hoch wie bei der Duplikateliminierung. Auch hier lässt sich Phase 1 wieder optimieren, indem man die Aggregation schon auf die Teillisten anwendet. Diese “Pre-Aggregation” ist besonders wichtig bei verteilten DBMS.

4.4.3. Vereinigung (binär)#

Bei der Vereinigung werden zwei Relationen \(R\) und \(S\) eingelesen und in sortierte Teillisten geschrieben. Der Sortierschlüssel ist das gesamte Tupel. Dann lesen wir jeweils einen Block aus den Mengen sortierter Teillisten, suchen das kleinste Tupel, geben dieses aus und entfernen es auch aus allen anderen Teillisten. Zur Not müssen wir wieder Blöcke nachladen. Als nächstes holen wir uns wieder jeweils einen Block aus beiden Mengen sortierter Teillisten und suchen das kleinste Tupel.
Dieser Algorithmus funktioniert für Mengen und Multimengen, bei letzterem eignen sich One-Pass Algorithmen aber besser. Die I/O-Kosten betragen \(3 · (B(R) + B(S))\) da jede Relation dreimal gelesen wird. Damit liegt die maximale Größe bei \(B(R) + B(S) ≤ M²\).

4.4.4. Schnittmenge und Differenz#

Der Algorithmus für die Schnittmenge und die Differenz ist im Grunde derselbe wie bei der Vereinigung. Allerdings müssen wir hier für jede Relationen zählen, wie häufig ein Tupel vorkommt. Die Ausgabe hängt dann vom Operator ab. Bei der Schnittmenge von \(R\) und \(S\) in Mengensemantik \((R\cap_{S}S)\) geben wir ein Tupel \(t\) aus, wenn es in \(R\) und \(S\) vorkommt. Bei der Schnittmenge in Multimengensemantik \((R\cap_{B}S)\) wird ein Tupel mit dem niedrigsten COUNT-Wert COUNT-mal ausgegeben \((min(count(R,t), count(S,t))\). Bei der Differenz in Mengensemantik \((R-_{S}S)\) wird \(t\) nur dann ausgegeben, falls es in \(R\) vorkommt, aber nicht in \(S\) und bei der Multimengensemantik \((R-_{B}S)\) wird ein Tupel maximal so oft ausgegeben, wie es in \(R\), minus dem vorkommen in \(S\), vorhanden ist. Im Anschluss sucht man wieder das nächstkleinere Tupel und gibt dieses wieder, abhängig vom Operator, aus. Die I/O-Kosten sind auch hier \(3 · (B(R) + B(S))\).

4.4.5. Einfacher, Sort-basierter Join Algorithmus#

Folgendes Problem begegnet uns jetzt: Bei einem Join möchten wir alle Tupel mit gleichem Joinattributwert gleichzeitig im Hauptspeicher haben. Die Idee hierbei ist, so viel Speicher wie möglich für das aktuelle Jointupel zu reservieren, indem der Speicherbedarf anderer Algorithmusteile reduziert wird.

Wir haben die Relationen \(R\) und \(S\) und joinen diese auf \(Y ( R(X, Y) ⋈ S(Y, Z) )\). In der ersten Phase sortieren wir die beiden Relationen mit TPMMS und geben das sortierte Ergebnis aus. In Phase 2 werden \(R\) und \(S\) dann gemerged. Man lädt jeweils einen Block aus jeder Relation und sucht das kleinste \(Y\). Falls dies nicht im jeweils anderen Block vorkommt, werden alle Tupel mit diesem \(Y\) entfernt, andernfalls werden alle Tupel mit diesem \(Y\) identifiziert und man macht mit dem nächsten Block weiter. Am Ende gibt man alle Kombinationen aus.

Kosten

Wie sich die Kosten für den einfachen sort-basierten Join Algorithmus ergeben schauen wir uns an einem Beispiel an, dass wir schon bei Nested Loop Joins verwendet haben. Wir haben 1000 Blöcke in \(R\), 500 Blöcke in \(S\) und Platz für 101 Einheiten im Hauptspeicher. Für den TPMMS brauchen wir \(4 · B(R) + 4·B(S)\) = 4 · 1500 = 6000 I/O-Operationen. Für das mergen von \(R\) und \(S\) müssen wir diese noch einmal lesen und brauchen somit nochmal 1500 I/O-Operationen. Dafür benötigen wir nur 2 Blöcke im Hauptspeicher. In die restlichen 98 müssen dann alle Tupel mit einem bestimmten \(Y\)-Wert passen. Insgesamt brauchen wir dann \(5(B(R) + B(S))\) = 7500 I/O-Operationen. Die Hauptspeicherkapazität beträgt \(B(R) ≤ M²\) und \(B(S) ≤ M²\).

Als wir uns dieses Beipiel für Nested Loop Joins angeschaut haben, haben wir nur 5500 I/O-Operationen gebraucht. Das liegt daran, dass wir eine Relation geladen haben und die restlichen 500 Blöcke nachladen konnten. Nested loop joins sind außerdem quadratisch \(\frac{B(R)B(S)}{M}\) während der sort-based join linear ist. Etwas optimierter lässt sich letzterer aber schon darstellen. Die Sortierung muss nicht vollständig durchgeführt werden. Die Teillisten allein reichen auch. Damit spart man sich eine I/O-Operation in der zweiten Phase und rechnet nur noch \(3(B(R) + B(S))\).

Erweiterung

Vorausgesetzt wird immer, das alle Tupel beider Relationen mit einem bestimmten \(Y\)-Wert in den Hauptspeicher passen. Ist das nicht der Fall und diese Tupel passen nur in \(M-1\) Blöcke, müssen wir den One-Pass join für diesen \(Y\)-Wert verwenden. Andernfalls können wir den Nested loop join durchführen. Eine Fallunterscheidung kann hier überflüssige I/O-Operationen vermeiden.

Verbesserung des Sort-basierter Join Algorithmus

Kommen wir nun zu der Optimierung des sort-basierten Join Algorithmus. Die Idee hierbei ist, die zweite Phase des TPMMS mit dem Joinen zu verknüpfen. Das heißt, wir führen nur die erste Phase aus. Wir generieren also wieder Teillisten der Größe \(M\) für \(R\) und \(S\) mit \(Y\) als Sortiertschlüssel. Dann laden wir die ersten Blöcke aller Teillisten, suchen den kleinsten \(Y\)-Wert und erzeugen ein Jointupel. Die Annahme hierbei ist, dass alle Teillisten und auch alle Tupel mit gemeinsamen Y-Werten in den Hauptspeicher passen.

Schauen wir uns wieder ein bekanntes Beispiel an. Wir haben 1000 Blöcke in \(R\), 500 Blöcke in \(S\) und 101 Einheiten Platz im Hauptspeicher. In Phase 1 bekommen wir 10 Teillisten für \(R\) und 5 Teillisten für \(S\). Damit haben wir dann in Phase 2 15 Blöcke im Hauptspeicher und noch 86 Blöcke frei. Zusammen ergeben sich daraus \(3(B(R) + B(S))\) = 4500 I/O-Operationen. Oft sind noch viele Speicherblöcke übrig, da \(B(R)+B(S) << M²\).

4.4.6. Zusammenfassung – sortbasierte, two-pass Algorithmen#

In der Folgenden Abbildung 4.11 einmal ein Überblick über den Hauptspeicherverbrauch der jeweiligen Operatoren und deren I/O-Kosten.

../_images/Zusammenfassung-sort-basierte-Algorithmen_2.png — Fig. 4.11 Überblick über die sortbasierten, two-pass Algorithmen#

4.5. Hash-basierte Two-Pass Algorithmen#

Wir schauen uns jetzt Hash-basierte Varianten von Two-Pass Algorithmen und damit weitere Möglichkeiten Tupel zusammenzubringen an.

Auch bei Hash-basierten Two-Pass Algorithmen können wir wieder davon ausgehen, dass nicht der gesamte Input in den Hauptspeicher passt. Die Idee hierbei ist jetzt, alle Inputargumente zu hashen. Das bedeutet, alle Tupel, die man gemeinsam betrachten möchte, mit dem gleichen Hashwert auszustatten und sie in den selben Bucket zu stecken. Wenn man solche Gruppierungen von Tupeln hat, kann man für unäre Operatoren einen Bucket nach dem anderen abarbeiten. Für binäre Operatoren behandelt man Buckets, die aus jeder Relation zusammengehörige Tupel enthalten, paarweise. Dann muss man nicht alle Tupel betrachten, sondern nur die eines bestimmten Buckets. Anders als bei der Indexierung, die wir uns auch schon angeschaut haben und wo ein Bucket ein Block war, können wir davon ausgehen, dass bei diesem Verfahren in einen Bucket normalerweise mehr als ein Block passt.

Nun stellt sich die Frage, warum hashed man überhaupt? Dies macht man, um den Speicherbedarf zu reduzieren, indem man bestimmte Tupel vorsortiert und dann systematisch nachlädt. Möchte man unterschiedlich hashen, kann man maximal \(M\) Buckets gleichzeitig im Hauptspeicher haben. Wenn wir aber sagen, \(M\) ist die Anzahl der Blöcke, dann bedeutet das, dass ich jeweils einen Block pro Bucket als Repräsentant des Buckets im Hauptspeicher habe.

Damit wir später die One-Pass Regel pro Bucket einhalten können, müssen wir sicherstellen, dass ein ganzer Bucket in den Hauptspeicher passt.

4.5.1. Partitionierung mittels Hashing#

Hashing ermöglicht Partinionierung. Das bedeutet, Tupel mit gleichen Eigenschaften kommen zusammen in eine Partition, einen Bucket, eine Gruppe oder ein Cluster.

Wir haben \(M\) Speicherblöcke und wollen unsere Relation \(R\) auf \(M-1\) Buckets aufteilen. Im Optimalfall hat jeder Bucket ungefähr die selbe Größe. Außerdem möchten wir ja, dass jeder Bucket durch einen Speicherblock repräsentiert wird. Ist ein Speicherblock voll, können wir diesen auf die Disk schreiben und wieder auffüllen. Der letzte Speicherblock dient hier nur dem Einlesen der Tupel. Wir können ein Tupel nicht direkt in einem Bucket hashen, da wir dafür erst den ganzen Block lesen müssen. Haben wir das getan, können wir das Tupel hashen.

Die Idee der Partitionierung ist einfach. Für jedes Tupel aus \(R\) berechnen wir den Hashwert \(h(t)\) und bewegen es in den entsprechenden Bucket. Ist der Block, in dem sich dieser Bucket befindet, voll, scheiben wir den Block als Overflowblock auf die Disk. Am Ende schreiben wir auch alle anderen Blöcke auf die Disk. Dadurch können wir dann, wenn wir einen Bucket benötigen, diesen direkt laden. Jedoch müssen wir natürlich auch wissen, wo dieser Bucket zu finden ist.

Schauen wir uns hier zu einmal den Algorithmus an. Zuerst initialisieren wir \(M-1\) Buckets mit \(M-1\) Buffer (ein Block bleibt für das Lesen übrig). Für jeden Block der Relation \(R\) lesen wir \(B\) in den letzten leeren Block. Dann überprüfen wir für jedes Tupel aus diesem Block den Hashwert. Ist in dem Bucket mit dem passenden Hashwert noch Platz, kommt das Tupel hinein. Andernfalls wird der Buffer geleert und auf die Disk geschrieben. Am Ende werden die übrigen Buckets die noch im Speicher sind auch auf die Disk geschrieben. Damit sind die Daten partitioniert.

initialize M-1 buckets using M-1 empty buffers;
FOR each block b of R DO BEGIN
    read block b into M-th buffer
    FOR each tuple t in b DO BEGIN
        IF buffer for bucket h(t) has no room for t THEN
            BEGIN
                copy the buffer to disk; /* spill */
                initialize a new empty block in that buffer;
            END;
        copy t to buffer for bucket h(t);
    END;
END;
FOR each bucket DO
    IF the buffer for this bucket is not empty THEN
        write the buffer to disk;
        

4.5.2. Duplikateliminierung \(\delta(R)\)#

Es gibt Momente, in denen wir ein ganzes Tupel oder auch bestimmte Projektionen pro Tupel hashen wollen und sicher sein müssen, dass unterscheidbare Werte enthalten sind für beispielsweise Schlüsselattribute. Wenn wir ein Schlüsselattribut haben, gehen wir normalerweise davon aus, dass dieser Wert nur einmal auftaucht. Theoretisch kann es aber immer mal vorkommen, dass Duplikate zu finden sind und diese entfernt werden müssen.

Die Idee bei der Duplikateliminierung ist, dass gleiche Werte im selben Bucket landen. Dann können wir jeden Bucket einzeln betrachten, die Duplikate eliminieren und ein Tupel pro Bucket ausgeben.

Es kann sein, dass durch die Kollision unterschiedliche Tupel im selben Bucket landen. Deshalb können wir nicht von vornherein ein Tupel pro Bucket reservieren. Wir können aber annehmen, dass alle Blöcke eines Buckets in den Hauptspeicher passen und wir dann im Nachhinein einen One-Pass Algorithmus pro Bucket ausführen können. Dementsprechend können wir, wenn wir die Daten gleich verteilt haben, davon ausgehen, dass jeder Bucket ungefähr \(\frac {B(R)}{(M−1)}\) Blöcke enthält. Damit darf unser \(R\) maximal \(M(M−1)\) viele Blöcke groß sein, damit wir die Duplikateliminierung hier anwenden können. Dies lässt sich optimieren, indem wir beim hinzufügen in jedem Bucket überprüfen, ob nur DISTINCT Tupel in den Hauptspeicher passen.

Die I/O-Kosten für die Duplikateliminierung betragen \(3 · B(R)\). Ist die Relation geclustered gespeichert, lesen wir erst mal jeden Block der Relation ein und hashen diese in einen Bucket. Sind wir noch nicht dazu gekommen, Duplikate zu entfernen, müssen wir den Block auf die Disk schreiben und den Bucket noch einmal lesen.

4.5.3. Gruppierung und Aggregation \(\gamma_{L}(R)\)#

Die nächste Operation, die wir uns anschauen, ist die Gruppierung und Aggregation. Die Idee ist die selbe wie zuvor auch, jedoch hängt unsere Hashfunktion nun nur von den Gruppierungsattributen ab. Das Problem, dass hierbei auftreten kann, ist, dass wir nur sehr wenige DISTINCT Werte und damit auch nur sehr wenige, aber dafür sehr große, Buckets haben. In dem Fall müssen wir aufpassen, dass trotzdem noch ein Bucket in den Hauptspeicher passt, denn wir brauchen immernoch einen One-Pass Algorithmus pro Gruppe auf jedem Bucket.

Der Hauptspeicherbedarf beträgt wieder \(B(R) ≤ M²\), wir brauchen aber vermutlich viel weniger, da wir nur ein Tupel pro Gruppe/Bucket im Hauptspeicher haben. Die I/O-Kosten betragen auch hier wieder \(3 · B(R)\).

4.5.4. Mengenoperationen#

Bei binären Operationen haben beide Inputs die gleiche Hashfunktion. Bei Mengenvereinigungen hashen wir \(R\) und \(S\) jeweils auf \(M-1\) Buckets. Damit haben wir alle DISTINCT Werte und können die Bucketpaare, die zueinander passen, aus jeder Relation nehmen und vereinen. Auch hier können wir wieder einen One-Pass Algorithmus anwenden. Bei der Multimengenvereinigung müssen wir nicht hashen, wir können einfach jedes Tupel weiterreichen.

Der Speicherbedarf beträgt \(min(B(R), B(S)) ≤ (M−1)²\). Warum ist das so? Nun, wir möchten eine Relation im Hauptspeicher halten, während wir von der anderen die entsprechenden Buckets nachladen. Damit muss nur die kleinere Relation in den Hauptspeicher passen. Das muss auch für verschiedenen One-Pass Varianten gegeben sein.

Die I/O-Kosten setzten sich wie folgt zusammen. Die erste Relation müssen wir einmal lesen und schreiben. Die zweite Relation müssen wir auch einmal lesen und dann die Buckets eventuell auf die Festplatte schreiben, sollten diese voll sein. Die Pointer der Buckets aus der zweiten Relation behalten wir im Hauptspeicher. Müssen wir dann aus der neuen Relation ein Bucket laden, müssen wir das auch für die zweite Relation tun. Das heißt, wir müssen wieder schreiben, lesen und wieder schreiben pro Relation. Damit kommen wir auf \(3·(B(R) + B(S)) \ I/O-Kosten\).

4.5.5. Hashjoin#

Der Algorithmus des Hashjoin ist im Prinzip derselbe wie bei der Mengenvereinigung. Hier sind aber unsere Joinattribute die Hashschlüssel. Die Idee ist, dass Tupel mit gleichen Joinattributen im korrespondierenden Bucket landen. Dann kann man eine One-Pass Join Variante für jedes Bucket Paar durchführen.

Schauen wir uns das anhand eines Beispiels an. Wir haben 1000 Blöcke in Relation \(R\), 500 in \(S\) und 101 Einheiten Platz im Hauptspeicher. Es würden ca. 10 Blöcke der Relation \(R\) und ca. 5 Blöcke der Relation \(S\) in ein Bucket passen. Hier wählen wir den kleinsten Wert, also 5, und können dann einen One-Pass Algorithmus anwenden: Wir holen uns den ersten \(S\)-Bucket in den Hauptspeicher. Dann joinen wir Blöcke des passenden \(R\)-Buckets hinzu und holen uns den nächsten \(S\)-Bucket, usw.

Für das Hashing benötigen wir 1500 I/O-Operationen und jeweils weitere 1500 um die Buckets zu schreiben und zu lesen. Insgesamt kommen wir auf \(3(B(R) + B(S))\) = 4500 I/O-Operationen. Genauso viele, wie bei der sort-basierten Methode. Aber: Es geht besser. Und wie das geht schauen wir uns im nächsten Abschnitt an.

4.5.6. I/O Einsparungen#

Um I/O-Operationen einzusparen, können wir versuchen, nicht-verwendeten Speicher besser zu nutzen. Zum einen, könnten wir mehr als einen Speicherblock pro Bucket verwenden. Dadurch schreiben wir zwar effizienter, jedoch bleiben die I/O-Kosten gleich. Zum anderen können wir einen Hybrid Hashjoin durchführen und versuchen zu vermeiden, dass wir alle Tupel noch einmal zwischenspeichern und auf die Disk schreiben. Dafür können wir beim Hashing der ersten Relation manche der Buckets komplett im Hauptspeicher halten. Bei diesen Buckets können wir dann beim lesen der zweiten Relation sicher sein, dass diese fertig sind, wenn ein Tupel auf einen dieser Buckets fällt. Damit haben wir dann die Größe dieser Buckets an I/O-Kosten gespart.

Wir behalten also für \(S\) \(m\) Buckets komplett im Speicher und für alle anderen nur einen Block als Repräsentant. Wenn wir dann \(R\) hashen, können wir alle Tupel, die in diesen ersten Buckets schon verjoinbar sind, sofort ausgeben. Alle anderen schreiben wir nur in einen Block und wenn dieser voll ist, schreiben wir den auf die Festplatte. In der zweiten Phase führen wir dann den eigentlichen Join durch.

4.5.7. I/O Einsparungen – Hybrid Hashjoin#

Beim Hybrid Hashjoin ist es wichtig, wie wir unser \(m\) wählen, damit wir den Hauptspeicher entprechend nutzen können und immer noch einen Block pro Repräsentant im Hauptspeicher haben.

Es müssen einige Voraussetzungen gelten, damit wir \(m\) wählen können. Angenommen wir brauchen insgesamt \(k\) Buckets für \(S\) (weil wir \(k\) unterschiedliche Joinattribute haben). Dann wollen wir \(m\) so auswählen, dass noch \(k - m\) Buckets abbildbar sind. Das heißt, wir brauchen \(k - m\) freie Blöcke im Hauptspeicher. Letztendlich muss also für die Wahl unseres \(m\)’s gelten, dass \(m\)-Mal die Anzahl der Blöcke von \(S\) durch die Gesamtverteilung pro Joinwert zusammen mit \(k - m\) übrigen Blöcken, in den Hauptspeicher passen \((( m · \frac {B(S)}{k} ) + 1 · (k – m) ≤ M )\). Diese übrigen Blöcke schreiben wir dann auf die Disk.

Wenn wir R hashen haben wir \(m\) vollständige Buckets für S im Hauptspeicher und je einen Block für die \(k - m\) Buckets von \(R\), sowie deren korrespondierende \(S\)-Buckets. Falls ein Tupel aus \(R\) in einem der \(m\) Buckets gehashed wird, kann man sofort einen Joinpartner suchen und diese ggf. auch direkt ausgeben. Sollte ein Tupel in einem der \(k - m\) Buckets gehashed werden gehen wir vor wie zuvor und schreiben diesen auf die Festplatte. In Phase 2 des Joins muss dieser nur noch auf \(k - m\) Buckets angewendet werden.

4.5.8. Hybrid Hashjoin – Analyse#

Wie viel spart man nun tatsächlich mit dem Hybrid Join ein? Für jeden Block den wir im Hauptspeicher halten sparen wir 2 I/O-Operationen pro Relation und das bei \(\frac{m}{k}\) Buckets. Wir wollen \(m\) Buckets im Hauptspeicher halten und haben insgesamt \(k\) Buckets. Wir haben dann eine Einsparung von \(2 (\frac{m}{k}) · (B(R) + B(S))\).

Da wir unsere Einsparung möglichst maximieren wollen müssen wir uns fragen, wie \(m\) und \(k\) zu wählen sind. Wir müssen uns also überlegen, wie viele Buckets wir erlauben und wie viele wir davon im Hauptspeicher halten können, während wir gleichzeitig darauf achten müssen, dass die Relation in den Hauptspeicher passt. Dafür gibt es einen Trick. Wir wählen \(m = 1\) und minimieren \(k\). Das heißt, ein Bucket soll vollständig in den Hauptspeicher passen, dementsprechend dürfen es aber nicht zu viele Buckets sein. Um Repräsentanten zu haben, müssen \(k - m\) Blöcke verwendet werden, während wir den Rest für ein Bucket verwenden.

Nun aber zu der Frage, wie man überhaupt die Gesamtanzahl der Buckets minimiert, also die Bucketgröße so wählt, dass nur ein Bucket in den Hauptspeicher passt. Bei einer Bucketgröße von \(M\) rechnen wir \(k = \frac{B(S)}{M}\). Damit ist nur Platz für ein Bucket im Hauptspeicher \((m = 1)\). In der Realität ist die Bucketgröße allerding etwas kleiner, sodass wir auch den Rest abbilden können.

Rechnen wir mit den Formeln weiter und setzen für \(m\) und \(k\) ein, ergeben sich daraus unsere Einsparungen:
2 \((\frac{m}{k}) · (B(R) + B(S)) = 2 (\frac{1}{\frac{B(S)}{M}}) · (B(R) + B(S)) = (\frac{2M}{B(S)}) · (B(R) + B(S))\)

Die I/O-Kosten betragen dann \((3 - (\frac{2M}{B(S)})) · (B(R) + B(S))\). Man sieht also, dass es sinnvoller ist, wenige große Buckets anstatt viele kleine zu wählen.

Hybrid Hashjoin – Beispiel

Die vorherige Rechnung schauen wir uns nun anhand eines Beispiels genauer an. Wir haben 1000 Blöcke in \(R\), 500 Blöcke in S und 101 Einheiten Platz im Hauptspeicher. Wir wollen wieder einen Bucket im Hauptspeicher halten und rechnen mit \(k = \frac{B(S)}{M} = \frac{500}{101}\). Damit kommen wir auf 5 Buckets. Jeder Bucket hat dann ca. 100 Blöcke. Das würde aber bedeuten, dass wir für jeden Bucket den wir in den Hauptspeicher laden, 104 Einheiten benötigen. Die Restblöcke und einen Block fürs lesen müssen wir nämlich auch berücksichtigen. Wir haben aber nur 101 Einheiten zur Verfügung, also ist unser \(k\) zu klein. Das ist aber kein Problem, denn wir können iterativ unser \(k\) erhöhen und setzten dieses für unser Beispiel nun auf 6. Dann haben wir jeweils einen Puffer für die ersten fünf Buckets, einen für das Lesen der Relation und 95 Puffer für den letzten Bucket. Unsere erwartete Größe pro Bucket beträgt dann \(\frac{500}{6}\) ≈ 83.

Die Kosten für das Lesen von \(S\) in Phase 1 setzen sich zusammen aus 500-mal lesen und 417-mal schreiben, da wir einen Bucket im Hauptspeicher halten. Lesen wir \(R\), lesen wir 1000-mal. Schaut man sich das Verhältnis von 5 aus 6 an, müssen wir dann aber nur noch 833-mal schreiben.

Wenn wir in Phase 2 dann alle geschriebenen Blöcke noch einmal lesen kommen wir auf 1250 Blöcke. Zusammen ergibt das 500 + 1000 + 2 · (417 + 833) = 4000 I/Os und damit haben wir hier weniger Operationen benötgt, als mit dem normalen Hash-join oder sort-merge join.

4.5.9. Zusammenfassung Hash-basierter Verfahren#

Hier sehen wir eine Übersicht über die Operatoren und ihre I/O-Kosten, sowie deren Hauptspeicherbedarf bei Hash-basierten Verfahren. Wir können in dieser Übersicht auch gut das bekannte Muster, dass der Hauptspeicherbedarf immer quadratisch zur Größe der Relation bzw. bei binären Operationen quadratisch zur Größe der kleineren Relation ist, sehen.

../_images/Zusammenfassung-Hashbasierte-Verfahren.png — Fig. 4.12 Überblick über die Hashbasierten Verfahren#

Wdh.: Sort-basierte, two-pass Algorithmen

Zum Vergleich haben wir hier noch einmal eine Übersicht über die verschiedenen Operatoren der Sort-basierten Two-Pass Algorithmen, sowie auch hier deren Hauptspeicherbedarf und I/O-Kosten. Man kann insbesondere sehen, dass der sort-merge join die gleiche Laufzeit wie der Hash-join hat und beide damit dem Hybrid Hashjoin unterlegen sind.

Vergleich Hash-basierte und Sort-basierte Algorithmen

Der Speicherbedarf sowie die I/O-Kosten sind bei beiden Algorithmen ähnlich. Hash-basierte Algorithmen sind in der Regel aber platzsparender als Sort-basierte, da der Speicherbedarf nur vom kleineren der beiden Inputs abhängt. Die I/O-Kosten hängen beim Hash-basierten Verfahren von der Anzahl der Buckets und der Verteilung der Daten ab. Hat man Buckets die groß genug sind und gleichmäßig verteilte Daten, so kann dieser Algorithmus effizient sein. Sort-basierte Algorithmen produzieren oft einen sortierten Output, sodass sortierte Teillisten hintereinander auf die Disk geschrieben werden können. Das spart bei einer I/O-Operation Seektime. Haben wir viel Platz im Hauptspeicher, können auch mehrere Blöcke einer Liste auf einmal gelesen werden. Gleiches gilt auch bei Hash-basierten Verfahren, falls die Anzahl der Buckets nicht die im Hauptspeicher verfügbare Anzahl an Einheiten überschreitet.

4.6. Index-basierte Algorithmen#

Mit Index-basierten Verfahren haben wir die Möglichkeit unterschiedlich zu rechnen und zwar je nachdem ob wir eine clustered relation haben oder einen clustering index. Dies gilt insbesondere für Selektionen aber auch Joins und binäre Operationen. Ist unsere Relation geclustered gespeichert, haben wir Tupel auf möglichst wenig Blöcken auf der Disk. Diese Tupel sind in der Regel anhand ihres Primärschlüssels geclustered. Beim clustering index haben wir einen Index, der versucht, die Tupel so zu organisieren, dass Tupel mit gleichen Attributwerten möglichst zusammen sind, also auf möglichst wenig Blöcken. Das hat den Vorteil, dass man weniger Blöcke lesen und nicht zu jedem mehrmals springen muss. Eventuell kommt ein weiterer Block für das Layout hinzu. Oft liegt die Relation bereits geclustered vor, mit einem clustering index auf dem Primärschlüssel. Da nur anhand eines Attributs sortiert und gruppiert werden kann, kann man nur einen clustering index haben. Alle anderen Indizes müssen non-clustering indexes sein, denn diese speichern nur Pointer zu den Tupeln.

4.6.1. Index-basierte Selektion#

Mit dem Basisalgorithmus lesen wir die gesamte Relation ein und überprüfen die Bedingung. Ohne Index ist das die beste Methode. Liegt die Relation geclustered vor, betragen die I/O-Kosten \(B(R)\), ansonsten \(T(R)\). Haben wir jedoch einen Index, gehen wir davon aus, dass bei den Berechnungen die Werte gleich verteilt sind. Rechnen wir die Anzahl der distinct Werte geteilt durch die Anzahl der Blöcke, bekommen wir als Ergebnis die Anzahl der Blöcke die wir lesen müssen und damit unsere I/O-Kosten \((\lceil\frac{B(R)}{V(R,a)}\rceil)\). Diese können unter Umstände höher sein. Für den Index selbst zum Beispiel oder vielleicht weil die Tupel nicht perfekt auf die Blöcke verteilt sind, die Blöcke nicht vollgepackt wurden oder weil fremde Tupel auf den Blöcken sind.

Wichtig ist aufzurunden. Das machen wir insbesondere, wenn die Anzahl der distinct Werte der Anzahl der Tupel entspricht. Dann bekommen wir ein Ergebnis, dass kleiner als 1 ist und müssen aufrunden, um mindestens einen Block zu bekommen.

Haben wir nicht-Cluster Indizes ist im schlimmsten Fall jedes Tupel auf einen anderen Block verteilt. Unsere I/O-Kosten basieren dann auf \(T(R)\) und nicht \(B(R)\). Dann sieht die Formel wie folgt aus: \(\lceil\frac{T(R)}{V(R,a)}\rceil\). Auch hier können wieder zusätzliche I/O-Kosten für beispielsweise die Indizes anfallen. Besser wäre es, wenn zufällig mehr als ein Tupel auf dem Block wären.

Index-basierte Selektion – Beispiel

Schauen wir uns die Index-basierte Selektion an einem Beispiel an. Wir haben 1000 Blöcke und 20000 Tupel in \(R\). Wir suchen nach dem Attribut \(a\), welches den Wert 0 hat. Verwenden wir keinen Index und ist \(R\) geclustered, müssen wir die ganze Relation lesen. Also brauchen wir 1000 I/O-Operationen. Ist \(R\) nicht geclustered brauchen wir sogar 20000 I/O-Operationen.
Haben wir einen clustering index und 100 distinct Werte benötigen wir \(\frac{1000}{100}\) = 10 I/O-Operationen. Bei einem non-clustering Index und 10 distinct Werten sind wir bei \(\frac{20000}{10}\) = 2000 I/O-Operationen. Es wird deutlich, dass es am besten ist eine clustered relation komplett einzulesen. Um uns einmal den Extremfall anzuschauen: Hätten wir 20000 distinct Werte bräuchten wir nur eine I/O-Operation.

4.6.2. Joining mit Index#

Wir haben folgenden Natural Join: \(R(X,Y) ⋈ S(Y,Z). Y\) ist das Joinattribut und wir können davon ausgehen, das \(S\) einen Index auf \(Y\) hat. Zunächst müssen wir jeden Block aus \(R\) lesen. Für jedes Tupel extrahieren wir dann den \(Y\)-Wert und verwenden den Index um das entsprechende \(S\)-Tupel zu finden.

Auch hier gibt es wieder verschiedene Möglichkeiten die Kosten zu betrachten. Ist \(R\) geclustered, haben wir \(B(R)\) Kosten für das Lesen von \(R\). Für jedes Tupel von \(R\) muss man durchschnittlich \(\frac{T(S)}{V(S,Y)}\) Tupel aus \(S\) lesen. Falls der Index nicht clustering ist, berechnet man die Kosten mit \(T(R) · \frac{T(S)}{V(S,Y)}\). Ist der Index clustering rechnet man mit \(T(R) · \frac{B(S)}{V(S,Y)}\), bzw. um es genauer zu nehmen, mit \(T(R) · max[ 1 , \frac{B(S)}{V(S,Y)}]\). Das domniert die Kosten von \(B(R)\), bzw. \(T(R)\).

Joining mit Index – Beispiel

Wir haben 1000 Blöcke und 10000 Tupel in \(R\) und 500 Blöcke und 5000 Tupel in \(S\). Das sind jeweils 10 Tupel pro Block. Außerdem haben wir 100 distinct \(Y\)-Werte in \(S ( V(S,Y) )\). Die Relation \(R\) ist geclustered und der Index auf \(Y\) in \(S\) ist clustering. Zunächst müssen wir \(R\) lesen und da die Relation geclustered vorliegt, brauchen wir 1000 I/O-Operationen. Nun müssen wir für jeded Tupel aus \(R\) ein passendes Tupel in \(S\) finden. Dafür brauchen wir \(10000 · \frac{500}{100}\) = 50000 I/O-Operationen.

Dies klappt besser, falls \(R\) sehr klein ist. Dann werden viele Blöcke von \(S\) gar nicht erst besucht und man muss nicht so viel lesen. Das ist ein Vorteil gegenüber Hash- und Sort-basierten Methoden, da dort immer alles betrachtet wird.

Joining mit sortiertem Index

Eine weitere Variante des Joins ist das joinen mit einem sortierten, dichtbesetzten Index. Damit müssten wir, wenn wir beispielsweise einen sort-merge join verwenden, vorher nur eine Relation sortieren. Haben beide Relationen einen sortierten Index auf \(Y\), müssen wir nur noch die Merge-Phase ausführen und können einen „Zig-Zag-Join“ verwenden. Dabei würden Tupel aus \(R\) ohne Joinpartner in \(S\) nie gelesen werden und umgekehrt.

Joining mit Indizes – Beispiel

Wir verwenden wieder die Werte aus dem vorherigen Beispiel und haben \(B(R) = 1000\), \(B(S) = 500\), \(T(R) = 10000\), \(T(S) = 5000\) und \(M = 100\). \(R\) und \(S\) sind beide geclustered, aber nur \(S\) hat einen sortierten Index auf \(Y\). Das bedeutet, wir müssen zuerst \(R\) vorsortieren. Da 10 Tupel in jeden Block passen, können wir \(R\) in 10 Teillisten sortieren. Dafür benötigen wir 2000 I/O-Operationen. Nun nehmen wir aus jeder Teilliste einen Block und noch einen Block aus \(S\). Dafür müssen wir \(R\) und \(S\) noch einmal komplett lesen und brauchen dafür 1500 I/O-Operationen. Insgesamt kommen wir auf 3500 I/O-Operationen. Immer noch weniger als zuvor, jedoch wird hier ein sortierter Index vorausgesetzt.

Hat \(R\) nun auch einen Index, ist das Sortieren der Relationen unnötig, da wir den Zig-Zag-Join anwenden können. Im schlimmsten Fall müssen wir aber trotzdem \(R\) und \(S\) komplett lesen und brauchen dann wieder 1500 I/O-Operationen. Bei wenigen Joinpartnern benötigen wir dann aber viel weniger I/O-Operationen.