Relationale Algebra
Contents
8. Relationale Algebra#
Die Relationale Algebra ist der wohl formalste Teil dieser Vorlesung.
Zuvor wurde über die Modellierung von Daten gesprochen und wie man relationale Datenbanken entwirft.
Jetzt geht es darum, die zuvor modellierte relationale Datenbank mit einer Sprache zu manipulieren bzw. neue Sichten darauf zu erstellen und an diese Anfragen zu stellen.
8.1. Einführung#
In den letzten Kapiteln wurde das Relationsschema mit Basisrelationen, die in der Datenbank gespeichert sind, behandelt. Jetzt geht es um „abgeleitete“ Relationenschemata mit virtuellen Relationen, die aus den Basisrelationen berechnet werden.
Die „abgeleiteten“ Relationsschemata werden durch Anfragen definiert.
Dafür benötigt man eine Anfragesprache. Anfragen sollen hierbei die Basis-Relationen nicht verändern, sondern neue Relationen generieren, die die erforderten Schemata besitzen.
Das Ergebnis einer Anfrage ist somit immer eine Relation.
8.1.1. Kriterien für Anfragesprachen#
Für Anfragesprachen gibt es verschiedene Kritieren.
Ad-Hoc-Formulierung Die Nutzenden sollen eine Anfrage formulieren können, ohne ein vollständiges Programm schreiben zu müssen. Wenn man ein neues Programm in einer Sprache wie Python schreibt, muss man Bibliotheken importieren, sich über Effizienz und Datenstrukturen Gedanken machen. Dies soll bei einer Anfragensprache nicht der Fall sein.
Standardisierung Eine Anfragesprache sollte einem Standard entsprechend und aus einer minimalen Menge von Vokabularien bestehen. Dennoch besteht der SQL-Standard aus mehr als 1300 Seiten!
Deklarativität Ein weiteres Kriterium einer Anfragesprache ist die Deskriptivität bzw. die Deklarativität. Die Nutzenden sollen formulieren was sie haben möchten („Was will ich haben?“) und nicht wie das Ergebnis berechnet werden soll („Wie komme ich an das, was ich haben will?“). Das System erstellt die darunterliegenden Programme automatisch zu der gegebenen Anfrage, ohne dass man die Prozeduren des Programmablaufes beschreiben muss.
Optimierbarkeit Zusätzlich muss eine Anfrage optimierbar sein. Eine Sprache besteht aus wenigen Operationen. Für die Operatormenge gibt es Optimierungsregeln. Die Optimierung ist abhängig von der Nutzung bzw. von den Daten. Ein Operator kann entsprechend unterschiedlich teuer im Sinne der des Ressourcenverbrauches sein.
Effiziente Grundoperatoren Die Operatoren der Anfragesprache müssen effizient auszuführen sein. Im relationalen Modell hat jede Operation eine Komplexität ≤ \(O(n^2)\). Wobei \(n\) die Anzahl der Tupel einer Relation darstellt.
Abgeschlossenheit Die Abgeschlossenheit ist eine weitere Eigenschaft einer Anfragesprache. Das Ergebnis von Anfragen auf Relationen ist wiederum eine Relation und kann als Eingabe für die nächste Anfrage verwendet werden.
(Mengenorientiertheit) Eine weitere, aber nicht sehr strenge, Eigenschaft ist die Mengenorientiertheit. Die Operationen sollen auf Mengen von Daten definiert sein. Dies gilt aber nicht in jedem Fall. Letztendlich möchte man auf Elemente einer Tabelle zugreifen und nicht nur auf einzelne Elemente Datenpunkte, die zusammenhangslos vorkommen.
Angemessenheit ist eine weitere Eigenschaft einer Anfragensprache, die beschreibt, ob die Sprache auf das Datenmodell passt. Alle Konstrukte des zugrundeliegenden Datenmodells sollen unterstützt werden. Bei relationalem Datenmodell zählen Relationen, Attribute, Schlüssel, usw.
Vollständigkeit Die Vollständigkeit einer Anfragesprache gibt an, dass eine Sprache eine minimale Menge von Operatoren einer Standardsprache abdeckt. In Bezug auf das relationale Modell bedeutet das, dass mindestens die Anfragen einer der relationale Algebra ausgedrückt werden können.
Sicher Zuletzt soll eine Anfragesprache „sicher“ sein. Keine Anfrage, die syntaktisch korrekt ist, darf in eine Endlosschleife geraten oder ein unendliches Ergebnis liefern.
8.1.2. Anfragealgebra#
In der Mathematik ist die Algebra definiert durch einen Wertebereich und auf diesem definierte Operatoren.
Ein Operand besteht aus Variablen oder aus Werten, aus denen neue Werte konstruiert werden können (x, 2, 3, …).
Ein Operator besteht aus Symbolen, die Prozeduren repräsentieren, die aus gegebenen Werten neue Werte produzieren (+, -, * , /, …).
Für Datenbankanfragen gibt es ebenfalls eine Algebra, die relationale Algebra (RA). Sie ist eine Anfragesprache für das relationale Modell.
Die Inhalte der Datenbank (Relationen) sind die Operanden.
Die Operatoren definieren gewisse Funktionen zum Berechnen von Anfrageergebnissen.
Es sind sehr grundlegenden Dinge, die wir mit Relationen tun wollen.
8.1.3. Mengen vs. Multimengen#
Bei der relationalen Algebra geht es hauptsächlich um Mengen. Bei normalen Mengen darf kein Tupel doppelt auftauchen. Bei Multimengen können identische Tupel mehrmals vorkommen. Es kann nämlich in einer Datenbanktabelle passieren, dass die Schlüssel nicht ordentlich definiert sind. Dann hat man sozusagen ein „Sack voll mit Tupeln“ (engl. „bag“).
Die Operatoren der relationalen Algebra sind auf Mengen definiert, wohingegen die Operatoren auf einem DBMS (SQL-Anfragen) auf Multimengen definiert sind. Dies hat verschiedene Gründe. Zum Einem wird hiermit die Effizienz beeinflusst bzw. gesteigert. Dazu kann man sich überlegen wie man eine Vereinigung als Multimenge und eine Vereinigung als Menge implementiert.
8.2. Basisoperatoren#
Die Basisoperatoren der Relationalen Algebra werden in verschiedene Klassen eingeteilt. In diesem Unterkapitel wird zudem auf verschiedene Operatoren noch genauer eingegangen.
8.2.1. Klassifikation der Operatoren#
Die bereits bekannten Mengenoperatoren sind die Vereinigung, Schnittmenge und die Differenz. Hinzu kommen entfernende Operatoren. Diese werden auf einzelne Elemente angewandt. Dazu zählen Selektionen und Projektionen.
Mit kombinierenden Operatoren kann man mehrere Relationen miteinander verbinden und neue Kombinationen von Tupeln bilden. Im Gegensatz zu den Mengenoperationen bei denen die Ergebnistupel immer gleich aussehen, kann es bei den kombinierenden Operatoren dazu kommen, dass die Ergebnistupel in ihren Attributen unterschiedlich aussehen. Typische Operatoren dafür sind das Kartesische Produkt, ein Join bzw. die verschiedenen Joinvarianten.
Die Umbenennung ist die einzige Ooeration, die nicht die Tupel verändert, sondern das Schema.
Ein Ausdruck in der Relationlen Algebra besteht aus einer Kombination von Operatoren und Operanden, auch Anfragen (queries) genannt.
8.2.2. Vereinigung (union, \(\cup\))#
Die Vereinigung sammelt Elemente (Tupel) zweier Relationen unter einem gemeinsamen Schema auf.
R ∪ S := {t | t \(\in\) R \(\vee\) t \(\in\) S}
Um eine Vereinigung anwenden zu können, müssen die Attributmengen beider Relationen identisch sein. Dazu gehören die Namen, Typen und die Reihenfolge. Wenn man beispielsweise die Attribute in einer Tabelle in einem anderen Format hat als in der Anderen und die Werte vom gleichen Typ sind, kann mam diese Umbenennen und dennoch eine Vereinigung bilden.
Ein Element ist nur einmal in der Vereinigung von R und S (R ∪ S) vertreten, auch wenn es jeweils einmal in R und S auftaucht. Es kommt zu einer Duplikatentfernung.
Das Beispiel zeigt zwei Tabellen R und S mit jeweils Name, Adresse, Geschlecht und Geburt. Wenn man diese Relationen miteinander vereinigt, erhält man eine neue Relation, in der das Tupel mit “Carrie Fisher” nur ein Mal vorkommt.
|
|
\(R \cup S\)
Name |
Adresse |
Geschlecht |
Geburt |
|---|---|---|---|
Carrie Fisher |
123 Maple St., Hollywood |
F |
9/9/99 |
Mark Hamill |
456 Oak. Rd., Brentwood |
M |
8/8/88 |
Harrison Ford |
789 Palm Dr., Beverly Hills |
M |
7/7/77 |
8.2.3. Differenz (difference, ―, \)#
Die Differenz in der Relationalen Algebra ist sehr ähnlich zu der aus der Mathematik.
Die Differenz von R und S (R − S) eliminiert die Tupel aus der ersten Relation, die auch in der zweiten Relation vorkommen. Die Schemata beider Relationen müssen für eine Differenz gleich sein.
R − S := {t | t \(\in\) R \(\wedge\) t \(\notin\) S}
Die Kommutativität gilt bei der Differenz nicht:
R − S ≠ S − R
In dem folgendem Beispiel gibt es sowohl in der Relation R, als auch in der Relation S, das gleiche Tupel mit “Carrie Fisher”. Bei der Differenz (R-S) wird das in beiden vorkommende Tupel eliminiert.
|
|
\(R-S\)
Name |
Adresse |
Geschlecht |
Geburt |
|---|---|---|---|
Mark Hamill |
456 Oak. Rd., Brentwood |
M |
8/8/88 |
8.2.4. Schnittmenge (intersection, \(\cap\))#
Die Schnittmenge R \(\cap\) S ergibt die Tupel, die in beiden Relationen gemeinsam vorkommen.
R \(\cap\) S := {t | t \(\in\) R \(\wedge\) t \(\in\) S}
Die Schnittmenge als Operator kann durch Verinigungen und Differenzen dargestellt werden, daher ist sie prinzipiell „überflüssig“.
R \(\cap\) S = R − (R − S) = S − (S − R)
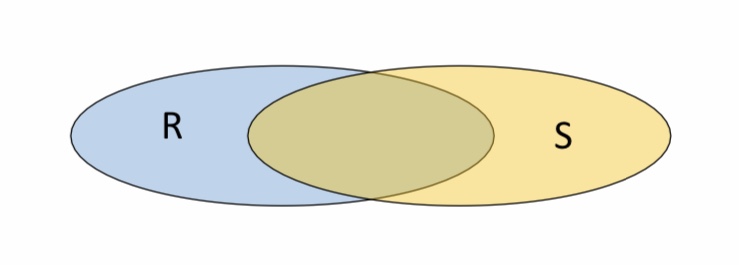
Das Beispiel dazu zeigt zwei Relationen R und S. In Relation R, sowie in Relation S, gibt es ein identisches “Carrie Fisher” Tupel. Bildet man die Schnittmenge der beiden Relationen (\(R\cap S\)), sind in der Ergebnisrelation alle Tupel, die sowohl in R, als auch in S vorkommen. In diesem Fall wäre es nur das Tupel mit “Carrie Fisher”.
|
|
\(R\cap S\)
Name |
Adresse |
Geschlecht |
Geburt |
|---|---|---|---|
Carrie Fisher |
123 Maple St., Hollywood |
F |
9/9/99 |
8.2.5. Projektion (projection, \(\pi\))#
Die Projektion ist ein unärer Operator. Sie erzeugt eine neue Relation mit einer Teilmenge der ursprünglichen Attribute.
Angenommen man projiziert auf eine Relation R mit den Attributen A1 bis Ak: \(\pi_{A1,A2,…,Ak}\)( R ). Als Ergbnis erhält man eine neue Relation mit einer Teilmenge der ursprünglichen Attribute von R. Die Reihenfolge der Attribute entspricht üblicherweise der aufgelisteten Reihenfolge.
Durch das Weglassen von Attributen, kann es dazu kommen, dass die übrig gebliebenen Attribute Duplikate enthalten. Diese werden implizit entfernt.
Ein Beispiel hierzu: Man bildet eine Projektion mit den Attributen A und B auf R. Das Ergebnis sind zwei identische Tupel. Das Duplikat wird eliminiert.
Relation R
A |
B |
C |
|---|---|---|
1 |
1 |
2 |
1 |
1 |
3 |
\(\pi_{A,B}\)( R )
A |
B |
|---|---|
1 |
1 |
Hier sind zwei weitere Beispiele zu Projektionen anhand einer Film-Tabelle dargestellt.
Im ersten Beispiel werden bei der Projektion nur die Spalten Titel, Jahr und Länge behalten. Die anderen Spalten werden weggeschnitten.
In zweitem Beispiel kommt ‘True’ doppelt vor und daher werden dessen Duplikate entfernt.
Film
Titel |
Jahr |
Länge |
inFarbe |
Studio |
ProduzentID |
|---|---|---|---|---|---|
Total Recall |
1990 |
113 |
True |
Fox |
12345 |
Basic Instinct |
1992 |
127 |
True |
Disney |
67890 |
Dead Man |
1995 |
121 |
False |
Paramount |
99999 |
\(\pi_{Titel,Jahr,Länge}\)(Film)
Titel |
Jahr |
Länge |
|---|---|---|
Total Recall |
1990 |
113 |
Basic Instinct |
1992 |
127 |
Dead Man |
1995 |
121 |
\(\pi_{inFarbe}\)(Film)
inFarbe |
|---|
True |
False |
8.2.6. Erweiterte Projektion#
Die Relationale Algebra erlaubt es den Projektionsoperator mehr Fähigkeiten zu geben. Bei der einfachen Projektion zuvor (\(\pi_{L}\)( R )) war das L dabei ‘nur’ eine Attributliste. Die erweiterte Projektion kann neben der Attributliste auch andere Ausdrücke an der Stelle des L’s stehen haben.
Ein anderer Ausdruck wäre A→B, wobei A ein Attribut in R und B ein neuer Name ist. Dies entspricht einer Umbenennung von Attributen.
Eine weitere Möglichkeit für einen neuen Ausdruck ist e→C. e ist ein Ausdruck mit Konstanten, arithmetischen Operatoren, Attributen von R, String-Operationen. C ist der neue Name für den Ausdruck e. Zwei Beispiele hierfür:
A1 + A2 → Summe
Vorname || ` ` || Nachname → Name
8.2.7. Selektion (selection, \(\sigma\))#
Ein weiterer unärer Operator ist die Selektion. Sie erzeugt eine neue Relation mit gleichem Schema, aber einer Teilmenge der Tupel. Einfach ausgedrückt kann man sagen, dass eine Selektion die Anzahl der Tupel reduziert.
Nur Tupel, die der Selektionsbedingung C (condition) entsprechen, werden in die neu erzeugte Relation übernommen. Für jedes Tupel wird somit einmal die Bedingung geprüft. Es handelt sich bei den Selektionsbedingungen um boolesche Selektionsbedingungen wie man sie aus Programmiersprachen kennt.
Die Operanden der Selektionsbedingung sind nur Konstanten oder Attribute von R. Diese können mittels Vergleichsoperatoren wie <, >, ≤, \(\ge\), <> und = verglichen werden. const = const ist ein Beispiel dafür wie so etwas aussehen kann. Ist aber eigentlich unnötig, da es sich um Konstanten handelt. Eine typische Selektion ist ein Vergleich zwischen Attribut und Konstante (attr = const). Wenn man zwei Attribute miteinander vergleicht, (attr = attr) kann man mögliche Attribute finden, an denen die zwei Relationen gejoint werden können. Das würde einer Join Bedingung entsprechen.
Die einzelnen Selektionsbedingungen können zu einer gesamten Selektionsbedingung durch AND, OR und NOT kombiniert werden.
Nicht zu verwechseln sind die Selektion aus der Relationalen Algebra mit dem SELECT aus SQL. Das SELECT entspricht in der Relationalen Algebra einer Projektion. Die Selektion wiederrum entspricht in SQL einer WHERE-Bedingung:
Selektion \(\neq\) SELECT
Die Beispiele zeigen verschiedene Selektionen auf einer gegebenen Film-Relation.
Im ersten Beispiel werden alle Filme selektiert, dessen Länge größer oder gleich 100 Minuten ist.
Im zweitem Beispiel kommt noch hinzu, dass diese Filem vom Fox-Studio produziert worden sein müssen.
Film
Titel |
Jahr |
Länge |
inFarbe |
Studio |
ProduzentID |
|---|---|---|---|---|---|
Total Recall |
1990 |
113 |
True |
Fox |
12345 |
Basic Instinct |
1992 |
127 |
True |
Disney |
67890 |
Dead Man |
1995 |
90 |
False |
Paramount |
99999 |
\(\sigma_{Länge\geq100}\)(Film)
Titel |
Jahr |
Länge |
inFarbe |
Studio |
ProduzentID |
|---|---|---|---|---|---|
Total Recall |
1990 |
113 |
True |
Fox |
12345 |
Basic Instinct |
1992 |
127 |
True |
Disney |
67890 |
\(\sigma_{Länge\geq100 AND Studio='Fox'}\)(Film)
Titel |
Jahr |
Länge |
inFarbe |
Studio |
ProduzentID |
|---|---|---|---|---|---|
Total Recall |
1990 |
113 |
True |
Fox |
12345 |
8.2.8. Kartesisches Produkt (Cartesian product, cross product \(\times\))#
Das Kartesische Produkt ist ein binärer Operator. Benannt worden ist es nach René Descartes. Ein französischer Naturwissenschaftler, Mathematiker und Philosoph. Das Kartesische Produkt ist auch unter anderen Namen wie Kreuzprodukt oder Produkt bekannt. Außerdem gibt es verschiedene Schreibweisen dafür: R * S statt R \(\times\) S
Das Kreuzprodukt zweier Relationen R und S ist die Menge aller Tupel, die man erhält, wenn man jedes Tupel aus R mit jedem Tupel aus S kombiniert. Das Schema hat ein Attribut für jedes Attribut aus R und S. Bei Namensgleichheit von zwei oder mehreren Attributen wird kein Attribut ausgelassen, stattdessen werden sie eindeutig umbenannt.

Das Beispiel zum Kartesischen Produkt zeigt zwei Relationen R und S, die mittels Kreuzprodukt kombiniert werden. Dazu werden alle möglichen Kombinationen der Tupel gebildet. Die Relationen R und S haben ein Attribut mit dem selben Namen (B). In der neuen Ergbnisrelation wird das Attribut jeweils eindeutig umbenannt. Bei der Umbennenung wird als Präfix der Relationsname vor das Attribut geschrieben: R.B und S.B.
\(R\)
A |
B |
|---|---|
1 |
2 |
3 |
4 |
\(S\)
B |
C |
D |
|---|---|---|
2 |
5 |
6 |
4 |
7 |
8 |
9 |
10 |
11 |
\(R \times S\)
A |
R.B |
S.B |
C |
D |
|---|---|---|---|---|
1 |
2 |
2 |
5 |
6 |
1 |
2 |
4 |
7 |
8 |
1 |
2 |
9 |
10 |
11 |
3 |
4 |
2 |
5 |
6 |
3 |
4 |
4 |
7 |
8 |
3 |
4 |
9 |
10 |
11 |
8.2.9. Der Join – Operatorfamilie#
Die folgenden Joins bilden eine Übersicht über die Joins, die in dieser Veranstaltung genauer betrachtet werden:
Natürlicher Join (natural join)
Theta-Join
Equi-Join
Semi-Join und Anti-Join
Left-outer Join und Right-outer Join
Full-outer Join
8.2.10. Natürlicher Join (natural join, ⋈)#
Der natürliche Join ist ein binärer Operator.
Beim Kreuzprodukt zuvor wurden alle möglichen Tupelpaare gebildet. Im Gegensatz dazu werden beim natürlichen Join Tupelpaare gebildet aus Tupeln, die „irgendwie“ übereinstimmen.
Es werden Tupel miteinander verbunden, die eine Übereinstimmung in allen gemeinsamen Attributen besitzen.
Somit handelt es sich dabei um einen „Verbund“ von Tupeln miteinander. Gegebenenfalls ist beim „Verbinden“ eine Umbennung der Attribute erforderlich. Zum Beispiel wäre dies erforderlich bei zwei Attributen in unterschiedlichen Relationen, wenn die Attribute das Selbe aussagen, aber unterschiedlich benannt worden sind.
Der natürliche Join arbeitet nach dem Schema: Vereinigung der beiden Attributmengen. Im Vergleich zum Kreuzprodukt gibt es nicht mehr die gleichen Attribute doppelt und umbenannt. Das Ergebnis ist nun eine Menge aus Attributen, also ohne (umbenannte) Duplikate.
Die Grafik zeigt passend dazu den natürlichen Join zwischen zwei Relationen. Die Rechtecke stellen Attribute und der Verbund von Rechtecken Relationen dar. Beide ursprünglichen Relationen bestehen aus zwei Attributen, wobei das orangene Attribut in beiden gleich ist. Die erste Relation (oben) besteht zusätzlich noch aus einem blauen und die zweite Relation (unten) aus einem grünen Attribut. Bei einem natürlichen Join beider Relationen wird über die identischen Attribute beider Relationen gejoint. In diesem Fall ist es das orangefarbene Attribut. Die Ergebnisrelation enthält somit am Ende das blaue, grüne und nur einmal das orangene Attribut.
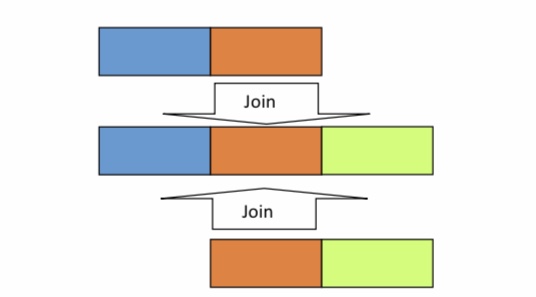
Beim natürlichen Join gibt es verschiedene Notationen.
r[A] beschreibt eine Projektion des Tupels r auf dem Attribut A. Es gibt somit genau den Wert des Tupels R beim Attribut A an.
Gegeben sind nun zwei Relationen R und S. Beide Relationen haben die gemeinsamen Attribute A1, …, Ak. Dann wird der natürliche Join wie folgt definiert:
R ⋈ S = {r \(\cup\) s | r\(\in\)R \(\wedge\) s\(\in\)S \(\wedge\) r[A1]=s[A1] \(\wedge\) … \(\wedge\) r[Ak]=s[Ak] }
Achtung: Bei der Verinigung von r und s handelt es sich also um Tupelwerte und nicht um Relationen!
Eine alternative, üblichere Definition ist eine Selektion auf dem Kreuzprodukt der Relationen R und S. Die Selektion hat dabei als Bedingung, dass die Werte gleicher Spalten, übereinstimmen. Dabei muss noch projiziert und umbenannt werden, um die Vereinigung richtig zu erwirken.
R ⋈ S = s r[A1]=s[A1] \(\wedge\) … \(\wedge\) r[Ak]=s[Ak](R × S)
Dazu ein Beispiel: Die ursprünglichen Tabellen sind R und S. Auf diesen beiden wird ein natürlicher Join ausgeführt. Dabei wird nur auf gleichen Attributen gejoint. In diesem Fall ist es das Attribut B. R und S stimmen in B in den Werten 2 und 4 überein. Das übrig gebliebene Tupel mit der 9 in B, muss somit nicht mehr kombiniert werden.
\(R\)
A |
B |
|---|---|
1 |
2 |
3 |
4 |
\(S\)
B |
C |
D |
|---|---|---|
2 |
5 |
6 |
4 |
7 |
8 |
9 |
10 |
11 |
\(R ⋈ S\)
A |
B |
C |
D |
|---|---|---|---|
1 |
2 |
5 |
6 |
3 |
4 |
7 |
8 |
Zur Erinnerung ist hier das kartesische Produkt der Relationen R und S dargestellt. Hierauf könnte man die alternative bzw. üblichere Definition des natürlichen Joins anwenden. Man würde wieder die gleichen zwei Tupel nach der Selektion erhalten. Zusätzlich müsste man noch R.B oder S.B wegprojizieren.
\(R \times S\)
A |
R.B |
S.B |
C |
D |
|---|---|---|---|---|
1 |
2 |
2 |
5 |
6 |
1 |
2 |
4 |
7 |
8 |
1 |
2 |
9 |
10 |
11 |
3 |
4 |
2 |
5 |
6 |
3 |
4 |
4 |
7 |
8 |
3 |
4 |
9 |
10 |
11 |
Bei dem zweiten Beispiel gibt es mehr als ein gemeinsames Attribut. Es stimmen in R und S die zwei Attribute B und C überein. B und C müssen somit gleichzeitig bei jedem Join übereinstimmen.
Obwohl der Wert von B (2) im ersten Tupel beider Relationen übereinstimmt, können diese nicht gejoint werden. Der Grund dafür sind unterschiedliche Werte (3 != 5) im Attribut C.
Das erste Tupel aus R und das zweite Tupel aus S haben wiederum in B und C die gleichen Werte und können somit gejoint werden. Genauso haben das zweite und dritte Tupel von R die gleichen Werte in B und C wie das dritte Tupel von S. Das dritte Tupel in S wird also mit mehr als einem Partner verknüpft.
|
|
\(R ⋈ S\)
A |
B |
C |
D |
|---|---|---|---|
1 |
2 |
3 |
5 |
6 |
7 |
8 |
10 |
9 |
7 |
8 |
10 |
8.2.11. Theta-Join (theta-join, \(⋈_\theta\))#
Der Theta Join ist die Allgemeinste Form der Joins. Der natürliche Join ist also ein Spezialfall vom Theta-Join.
Die Verknüpfungsbedingung kann selbst gestaltet werden. Zuvor war die Bedingung, dass die Attribute auf denen gejoint wird, gleich sind.
Das Ergebnis wird ähnlich wie zuvor konstruiert. Zunächst wird ein Kreuzprodukt der beiden Relationen gebildet. Selektiert wird darauf mittels der gegebenen Joinbedingung \(\theta\). Dabei ist A ein Attribut in R und B ein Attribut in S.
R ⋈\(A_\theta\) B S = s \(A_\theta\) B (R \(\times\) S)
\(\theta\) ∈ {=, <, >, ≤, ≥, ≠}
Das Schema der Ergebnisrelation eines Theta-Joins sieht wie das Schema vom Kreuzprodukt aus. Wenn die Joinbedingung der Operator „=“ ist, handelt es sich um einen Equi-Join. Dieser ist somit, wie auch der Natural-Join, ein Spezialfall des Theta-Joins. Der Unterschied zum Natural Join ist aber, dass das Schema des Ergebnisses anders aussieht als beim Equi-Join. Gleiche Attribute werden umbenannt und sozusagen zu einem Attribut zusammengefasst.
R(A,B,C) ⋈ S(B,C,D)
= \(\rho_{T(A,B,C,D)}\)(\(\pi_{A,R.B,R.C,D}\)(\(\sigma_{(R.B=S.B AND R.C = S.C)}\) (\(R \times S\))))
Im ersten Beispiel zum Theta-Join werden R und S gejoint, wenn der Wert vom Attribut A kleiner als der von D ist. Zunächst wird das erste Tupel von R mit allen Tupeln von S verglichen. In jedem Fall stimmt die Bedingung und die Tupel können verbunden werden. Analog werden die weiteren Tupel von R mit denen von S verglichen und gegebenenfalls verbunden.
|
|
\(R ⋈_{A<D}S\)
A |
R.B |
R.C |
S.B |
S.C |
D |
|---|---|---|---|---|---|
1 |
2 |
3 |
2 |
5 |
6 |
1 |
2 |
3 |
2 |
3 |
5 |
1 |
2 |
3 |
7 |
8 |
10 |
6 |
7 |
8 |
7 |
8 |
10 |
9 |
7 |
8 |
7 |
8 |
10 |
Im zweitem Beispiel wird die Bedingung erweitert. R.B und S.B dürfen nicht mehr gleich sein. Wie zuvor wird jede Zeile von R mit jeder Zeile von S verglichen und geprüft, ob die Bedingung stimmt. Falls ja, werden die Tupel miteinander verknüpft. Generell können Bedingungen beliebig lang werden.
\(R ⋈_{A<D \wedge R.B \neq S.B}S\)
A |
R.B |
R.C |
S.B |
S.C |
D |
|---|---|---|---|---|---|
1 |
2 |
3 |
7 |
8 |
10 |
8.2.12. Komplexe Ausdrücke#
Die Idee hinter komplexen Ausdrücken ist die Kombination (Schachtelung) von Ausdrücken zur Formulierung komplexer Anfragen.
Aufgrund der Abgeschlossenheit der relationalen Algebra kann der Output eines Ausdrucks, der immer eine Relation ist, als Input für den nächsten Ausdruck verwendet werden.
Die Darstellung von komplexen Ausdrücken erfolgt mittels Klammerung und Schachtelung von Ausdrücken. Die komplexen Ausdrücke können in einen Baum aufgespalten und dargestellt werden.
Film
Titel |
Jahr |
Länge |
Typ |
StudioName |
|---|---|---|---|---|
Total Recall |
1990 |
113 |
Farbe |
Fox |
Basic Instinct |
1992 |
127 |
Farbe |
Disney |
Dead Man |
1995 |
90 |
s/w |
Paramount |
Als Beispiel zu komplexen Ausdrücken sei hier eine Film-Relation gegeben. Gesucht werden Titel und Jahr von den Filmen, die von Fox produziert wurden. Die Filme sollen mindestens 100 Minuten lang sein.
Um die Beispielanfrage in die Relationale Algebra zu übersetzen, wird die Anfrage Stück für Stück durchgegangen und umgewandelt. In diesem Beispiel fangen wir von innen heraus an.
Gesucht werden Filme, die von Fox produziert worden sind. Somit wird eine Selektion mit der Selektionsbedingung StudioName=‘Fox’ auf der Film-Relation benötigt (\(\sigma_{StudioName=‚Fox‘}\)(Film)).
Die zweite Bedingung fordert, dass alle Filme mindestens 100 Minuten lang sind. Dafür wird wieder eine Selektion auf der Film-Relation angewandt \(\sigma_{Länge≥100}\)(Film).
Da beide Bedingungen gleichzeitig gelten sollen, nimmt man die Schnittmenge von den beiden zuvor verwendeten Selektionen (\(\sigma_{Länge≥100}\)(Film) \(\cap\) \(\sigma_{StudioName=‚Fox‘}\)(Film)).
Alternativ lässt sich als eine längere Selektionsbedingung darstellen. Dazu werden beide Bedingungen mit einem AND verknüpft (\(\sigma_{Länge≥100 AND StudioName=‚Fox‘}\)(Film)).
Da nach Titeln und Jahr gesucht wird, wird die Relation am Ende auf die Attribute Titel und Jahr noch projiziert (\(\pi_{Titel,Jahr}\)(…)).
Die vollständige Anfrage in Relationaler Algebra sieht wie folgt aus:
\(\pi_{Titel,Jahr}\)(\(\sigma_{Länge≥100}\)(Film) \(\cap\) \(\sigma_{StudioName=‚Fox‘}\)(Film)) oder in alternativer Form:
\(\pi_{Titel,Jahr}\)(\(\sigma_{Länge≥100 AND StudioName=‚Fox‘}\)(Film))
Generell gibt es aber viele verschiedene Möglichkeiten wie ein solcher Ausdruck formuliert wird.
Das folgende Beispiel zeigt wie ein Baum von innen heraus aufgespannt wird. Dabei wird mit der Film Relation und den Selektionen darauf begonnen. Danach werden die Ergebnisrelationen beider Selektionen durch eine Schnittmenge verbunden. Zuletzt wird durch die Projektion die Spalten Titel und Jahr ausgegeben.
\(\pi_{Titel,Jahr}\)(\(\sigma_{Länge≥100(Film)}\) \(\cap\) \(\sigma_{StudioName=‚Fox‘}\)(Film))
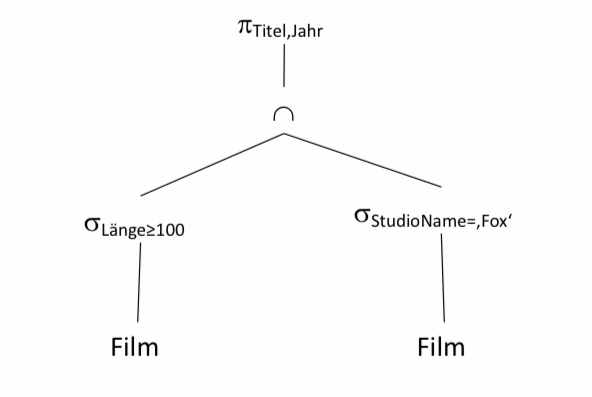
Zu der Alternative sähe der Baum dementsprechend anders aus. Er würde nur aus einer Film Relation, einer Selektion mit längerer Selektionsbedingung und einer Projektion bestehen. Letztendlich kommt bei beiden Ausdrücken die selbe Relation heraus.
\(\pi_{Titel,Jahr}\)(\(\sigma_{Länge≥100 AND StudioName=‚Fox‘}\)(Film))
Gegeben sind in diesem Beispiel zwei Relationen: Film und Rolle. Gesucht werden die Namen aller Schauspieler, die in den Filmen mitspielten, die mindestens 100 Minuten lang sind.
Die Schauspielernamen sind in einer anderen Tabelle als die Filme. Die Tabellen müssen irgendwie verlinkt werden. Dazu eignet sich die beiden Relationen (mittels einem natürlichen Join) zu joinen (Film ⋈ Rolle). Aus dieser Ergebnisrelation werden alle Filme selektiert, die mindestens 100 Minuten lang sind (\(\sigma_{Länge≥100}\)(…)). Da nur nach den Schauspielernamen gesucht wird, wird auf den Schauspielernamen projiziert (\(\pi_{SchauspName}\)(…)).
\(\pi_{SchauspName}\)(\(\sigma_{Länge≥100}\)(Film ⋈ Rolle))
Film
Titel |
Jahr |
Länge |
Typ |
StudioName |
|---|---|---|---|---|
Total Recall |
1990 |
113 |
Farbe |
Fox |
Basic Instinct |
1992 |
127 |
Farbe |
Disney |
Dead Man |
1995 |
90 |
s/w |
Paramount |
Rolle
Titel |
Jahr |
SchauspName |
|---|---|---|
Total Recall |
1990 |
Sharon Stone |
Basic Instinct |
1992 |
Sharon Stone |
Total Recall |
1990 |
Arnold |
Dead Man |
1995 |
Johnny Depp |
Zum Verständnis noch ein weiteres Beispiel:
Stud(Matrikel, Name, Semester)
Prof(ProfName, Fachgebiet, GebJahr)
VL(VL_ID, Titel, Saal)
Lehrt(ProfName, VL_ID)
Hört(Matrikel,VL_ID)
Gesucht werden in diesem Beispiel die unterschiedlichen Semester aller Studierenden, die eine Vorlesung eines Professors des Jahrgangs 1960 in Hörsaal 1 hören.
Zunächst muss überlegt werden, welche Relationen benötigt werden. Eine Bedingung ist, dass es Hörsaal 1 sein muss, in dem die Vorlesung gehört wird. Das Attribut Saal befindet sich in der Vorlesungsrelation (VL).
Der Jahrgang des Professors ist eine weitere Bedingung. Dafür wird die Professorrelation (Prof) benötigt.
Die Professorrelation lässt sich mit der Vorlesungsrelation über die Lehrtrelation (Lehrt) verbinden, da letztere aus jeweils einem Attribut der anderen beiden Relationen besteht.
Ansonsten wird nach den Semestern der Studierenden gefragt. Das Attribut Semester befindet sich in der Studierendenrelation (Stud). Um die Studierendenrelation mit den anderen Relationen zu kombinieren, benötigt man die Hörtrelation (Hört).
Nach dem Finden aller benötigten Relationen können nun die Selektionen auf den jeweiligen Relationen ausgeführt werden. Eine Bedingung war, dass der Professor vom Jahrgang 1960 sein muss. Diese Selektion wird direkt auf der Professorrelation ausgeführt. Die Bedingung, dass es Saal 1 ist, wird auf der gejointen Professor-, Lehrt- und Vorlesungsrelation durchgeführt. Dann werden die Hört- und die Studierendenrelation gejoint, um an die Semester der Studierenden zu kommen. Zum Schluss wird die Ergebnisrelation auf das Semester projiziert.
\(\pi_{Sem}\)(((\(\sigma_{Saal=1}\)(((\(\sigma_{GebJahr = 1960}\)(Professor))⋈Lehrt)⋈VL)⋈Hört)⋈Stud))
8.2.13. Umbenennung (rename, \(\rho\))#
Die Umbenennung ist ein unärer Operator. Sie dient zur Kontrolle der Schemata und bietet eine Möglichkeit einfachere Verknüpfungen anzuwenden.
In dem Beispiel wird eine Relation R in S und die Attribute in der neuen Relation in A1 bis An umbenannt:
\(\rho_{S(A1,…,An)}\)( R )
Hätte man das Selbe ohne die Attribute der neuen Relation, würde man nur die Relation umbenennen:
\(\rho_{S(R)}\)
Die Umbenennung ermöglicht weitere Operationen.
Wenn mehrere Tabellen, die die gleichen Daten besitzen, zusammengeführt werden sollen, benötigen sie die gleichen Schemata für die Mengenoperationen (Vereinigungen, Schnittmenge …). Eine Umbennung kann ein gleiches Schema herbeiführen.
Bei Joins, wo bisher kartesische Produkte verwendet wurden, können mit einer Umbenennung die unterschiedlichen Attribute gleich benannt und darüber gejoint werden.
Bei kartesischen Produkten, bei denen bisher Joins ausgeführt wurden, können gleiche Attribute unterschiedlich genannt werden.
In diesem Beispiel zum Operator Umbenennung sollen zwei Relationen R und S mittels dem Kreuzprodukt verbunden werden. Damit die Attribute B nicht gleich heißen, wird das B aus der S-Relation in X umbenannt.
\(R\)
A |
B |
|---|---|
1 |
2 |
3 |
4 |
\(S\)
B |
C |
D |
|---|---|---|
2 |
5 |
6 |
4 |
7 |
8 |
9 |
10 |
11 |
\(R \times \rho_{s(X,C,D)}(S)\)
A |
B |
X |
C |
D |
|---|---|---|---|---|
1 |
2 |
2 |
5 |
6 |
1 |
2 |
4 |
7 |
8 |
1 |
2 |
9 |
10 |
11 |
3 |
4 |
2 |
5 |
6 |
3 |
4 |
4 |
7 |
8 |
3 |
4 |
9 |
10 |
11 |
Alternativ können die Attribute der Ergebnisrelation erst nach dem Bilden des Kreuzproduktes von R und S umbenannt werden. Vor der Umbenennung sind die Namen der Attribute A, R.B., S.B, C, D und nach der Umbennung A, B, X, C, D.
\(\rho_{S(A,B,X,C,D)}\)(R \(\times\) S)
8.2.14. Unabhängigkeit und Vollständigkeit#
Man hat eine minimale Menge von Operationen, die die Relationenalgebra bilden. Mittels diesen Operationen kann auf alles wie z.B Joins, Schnittmengen, usw. abgebildet werden. Dazu gehören:
π, σ, \(\times\) , −, ∪ (und r)
Unabhängigkeit bedeutet, dass kein Operator dieser Menge weggelassen werden kann ohne die Vollständigkeit zu verlieren. Wäre die Menge nicht mehr vollständig und könnte nicht mehr auf alle Operatoren abgebildet werden.
Zum Beispiel sind der Natural Join, Join und die Schnittmenge redundant. Sie können durch andere Operatoren dargestellt werden:
R \(\cap\) S = R − (R − S)
R ⋈_C S = \(\sigma_C\)(R \(\times\) S)
R ⋈ S = \(\pi_{L}\)(\(\sigma_{R.A1=S.A1 AND … AND R.An=S.An}\)(R \(\times\) S))
Dennoch werden redundante Operatoren wie der Join häufig verwendet. Der Grund dafür ist die Übersichtlichkeit der Ausdrücke, wie man sehr gut am Beispiel für den natürlichen Join sehen kann.
8.2.15. Vorschau zu Optimierung#
Um Optimierung zu betreiben, müssen für die vorhandenen Ausdrücke äquivalente Umformungen bekannt sein, mit denen man sie gegebenenfalls austauschen kann.
Dazu ein paar Beispiele für algebraische Regeln bei der Transformation:
R gejoint mit S ist das Gleich wie S gejoint mit R. Die Reihenfolge der Attribute ist beim Tauschen von R und S eventuell anders. Kann im Nachhinein aber noch umsortiert werden.
R ⋈ S = S ⋈ R
Es gilt die Assoziativität. Die Reihenfolge der Klammerung kann beliebig getauscht werden. Das Ergebnis ändert sich auch dabei nicht.
(R ⋈ S) ⋈ T = R ⋈ (S ⋈ T)
Wenn man zwei Projektionen nacheinander durchführt und die äußere Projektion eine Teilmenge der inneren Projektion ist, kann die innere Projektion weggelassen werden.
\(\pi_{Y}(\pi_{X}(R)) = \pi_{Y}(R)\)
Falls Y ⊆ X
Angenommen man hat zwei Selektionen auf der gleichen Relation R. Dann kann die Reihenfolge beider Selektionen verändert werden. Alternativ können beide Selektionen auch als ein Ausdruck zusammengefasst und verknüpft werden. Das Ergebnis bleibt immer gleich, aber je nachdem was man zuerst ausführt können unterschiedliche Kosten entstehen.
\(\sigma_{A=a}(\sigma_{B=b}(R))= \sigma_{B=b}(\sigma_{A=a}(R)) [ = \sigma_{B=b\wedge A=a}(R) ]\)
Das Tauschen von einer Projektion mit einer Selektion ist möglich, sofern das Attribut A in X enthalten ist.
\(\pi_{X}(\sigma_{A=a}(R)) = \sigma_{A=a}(\pi_{X}(R))\)
Falls A ⊆ X
Die Selektion auf einer Vereinigung ist das Gleiche wie Selektionen auf den einzelnen Relationen, die dann vereinigt werden.
\(\sigma_{A=a}(R ∪ S) = \sigma_{A=a}(R) ∪ \sigma_{A=a}(S)\)
Der Optimierer fragt sich jedes Mal welche Seite besser bei der jetzigen Ausführung geeignet ist und wählt diese dann aus.
8.3. Operatoren auf Multimengen#
Mit dem Wissen über die Basisoperatoren der Relationalen Algebra, kann nun genauer auf die Multimengen eingegangen werden.
8.3.1. Motivation#
Mengen sind ein natürliches Konstrukt. Sie enthalten keine Duplikate. Mit dieser Annahme kann schnell eine Schlussfolgerung über einen Datensatz gezogen werden. In der Realität kommen in den Tabellen aber häufig Duplikate vor. Kommerzielle DBMS basieren daher fast nie nur auf Mengen und aus diesem Grund erlauben sie Multimengen. Eine Multimenge (bag, multiset) kann im Gegensatz zu einer Menge Duplikate enthalten.
A |
B |
|---|---|
1 |
2 |
3 |
4 |
1 |
2 |
1 |
2 |
Das Beispiel zeigt eine Multimenge, da (1,2) mehr als einmal in der Relation vorkommt. Die Reihenfolge der Tupel ist weiter unwichtig.
8.3.2. Effizienz durch Multimengen#
Bei manchen Operationen kann man durch die Nutzung von Multimengen Effizienz gewinnen.
Bei einer Vereinigung kann man die Daten direkt „aneinanderhängen“.
Bei einer Projektion kann man einfach die Attributwerte „abschneiden“. Es muss nicht wie bei Mengen sichergestellt werden, dass die Projektion keine Duplikate hat. Somit muss auch keine Duplikatsuchstrategie implementiert werden.
Die Suche nach Duplikaten ist sehr teuer. Jedes Tupel im Ergebnis muss mit jedem anderen Tupel verglichen werden. Die Kosten sind O(n²), nicht sehr effizient.
Eine Strategie effizienter nach Duplikaten zu suchen wäre es, alle Attribute zu sortieren. Die Kosten für eine Sortierung liegen in O(n log n) und sind somit günstiger als der Vergleich zuvor. Da man davon ausgeht, dass identische Tupel hintereinander in der sortierten Tabelle liegen, kann man die Tabelle nochmal durchgehen und dann Duplikate entfernen.
Bei der Aggregation kann eine Duplikateliminierung sogar schädlich bzw. unintuitiv sein. Angenommen man berechnet den Durchschnitt von A (AVG(A)) und bildet zunächst eine Projektion auf A. Das Ergebnis der Projektion in der Mengensemantik ist (1,3). Wohingegen das Ergebnis in der Mutlimengensemantik (1,3,1,1) ist. Häufig ist bei der Berechnung von einem Durchschnitt der Durchschnitt aller Werte gemeint. Die Mengensemantik kann also Verwirrung verursachen und die Betrachtung von Multimengen wäre sinnvoller.
Wenn in dem Beispiel eine Projektion auf (A,B) ausgeführt wird, erhält man in der Mutlimengensemantik alle Tupel aus (A,B). In der Mengensemantik wären es nur (1,2) und (3,4), ohne deren Duplikate.
A |
B |
C |
|---|---|---|
1 |
2 |
5 |
3 |
4 |
6 |
1 |
2 |
7 |
1 |
2 |
8 |
8.3.3. Vereinigung auf Multimengen#
Seien R und S jeweils eine Multimenge. Ein Tupel t erscheint n-mal in R und m-mal in S. Ein Tupel t erscheint in R \(\cup\) S genau (n+m) mal.
Im Beispiel kommt das Tupel (1,2) in R 3-mal und S nur 1-mal vor. Somit erscheint in R \(\cup\) das Tupel n+m = 3+1 = 4-mal.
|
|
\(R \cup S\)
A |
B |
|---|---|
1 |
2 |
3 |
4 |
1 |
2 |
1 |
2 |
1 |
2 |
3 |
4 |
3 |
4 |
5 |
6 |
8.3.4. Schnittmenge auf Multimengen#
Seien R und S jeweils eine Multimenge.
Ein Tupel t erscheint n-mal in R und m-mal in S.
Das Tupel t erscheint in R \(\cap\) S, dann genau min(n,m) mal.
Das Tupel (1,2) kommt in Relation R 3-mal und in S 1-mal vor. Somit erscheint es in R \(\cap\) S genau min(3,1) = 1-mal.
|
|
\(R\cap S\)
A |
B |
|---|---|
1 |
2 |
3 |
4 |
3 |
4 |
8.3.5. Differenz auf Multimengen#
Seien R und S jeweils eine Multimenge. Ein Tupel t erscheint n-mal in R und m-mal in S.
Das Tupel t erscheint in R − S dann genau max(0, n−m) mal.
Falls t öfter in R als in S vorkommt, bleiben n−m t übrig.
Falls t öfter in S als in R vorkommt, bleibt kein t übrig, da es keine Negativtupel gibt.
Jedes Vorkommen von t in S eliminiert ein t in R.
|
|
\(R -S\)
A |
B |
|---|---|
1 |
2 |
1 |
2 |
\(S-R\)
A |
B |
|---|---|
3 |
4 |
5 |
6 |
8.3.6. Projektion und Selektion auf Multimengen#
Bei der Projektion auf Multimengen können neue Duplikate entstehen. Diese werden nicht entfernt. Bei der Projektion (\(\pi_{A,B}(R)\)) im Beispiel werden daher die Duplikate des Tupels (1,2) nicht entfernt.
Bei der Selektion auf Mutlimengen wird die Selektionsbedingung auf jedes Tupel einzeln und unabhängig angewandt. Die schon vorhandenen Duplikate bleiben erhalten, sofern sie beide selektiert bleiben. Im Beispiel \(\sigma_{C\geq6}(R)\) wird somit nur das Tupel (1,2,5) entfernt, aber das Duplikat von (1,2,7) bleibt erhalten in der Ergebnisrelation.
\(R\)
A |
B |
C |
|---|---|---|
1 |
2 |
5 |
3 |
4 |
6 |
1 |
2 |
7 |
1 |
2 |
7 |
\(\pi_{A,B}(R)\)
A |
B |
|---|---|
1 |
2 |
3 |
4 |
1 |
2 |
1 |
2 |
\(\sigma_{C\geq6}(R)\)
A |
B |
C |
|---|---|---|
3 |
4 |
6 |
1 |
2 |
7 |
1 |
2 |
7 |
8.3.7. Kreuzprodukt auf Multimengen#
Seien R und S jeweils eine Multimenge. Ein Tupel t erscheint n-mal in R und ein Tupel u erscheint m-mal in S.
Das Tupel tu erscheint in R \(\times\) S dann genau n·m-mal.
\(R\)
A |
B |
|---|---|
1 |
2 |
1 |
2 |
\(S\)
B |
C |
|---|---|
2 |
3 |
4 |
5 |
4 |
5 |
\(R \times S\)
A |
R.B |
S.B |
C |
|---|---|---|---|
1 |
2 |
2 |
3 |
1 |
2 |
2 |
3 |
1 |
2 |
4 |
5 |
1 |
2 |
4 |
5 |
1 |
2 |
4 |
5 |
1 |
2 |
4 |
5 |
8.3.8. Joins auf Multimengen#
Bei Joins auf Multimengen gibt es keine großen Überraschungen. Der natürliche Join verbindet wieder zwei Relationen wo die Werte gleicher Attribute identisch sind. Der Theta-Join joint die Tupelpaare, bei denen die Selektionsbedingung erfüllt ist.
\(R\)
A |
B |
|---|---|
1 |
2 |
1 |
2 |
\(S\)
B |
C |
|---|---|
2 |
3 |
4 |
5 |
4 |
5 |
\(R⋈S\)
A |
B |
C |
|---|---|---|
1 |
2 |
3 |
1 |
2 |
3 |
\(R⋈_{R.B<S.B}S\)
A |
R.B |
S.B |
C |
|---|---|---|---|
1 |
2 |
4 |
5 |
1 |
2 |
4 |
5 |
1 |
2 |
4 |
5 |
1 |
2 |
4 |
5 |
8.4. Erweiterte Operatoren#
Die erweiterten Operatoren machen teilweise nur Sinn je nachdem, ob sie für Mengen oder für Multimengen definiert sind. Meistens ergibt sich aus dem Kontext welche Semantik vorliegt.
8.4.1. Überblick über Erweiterungen#
Eine kurze Übersicht zu den erweiterten Operatoren:
Duplikateliminierung
Aggregation
Gruppierung
Sortierung
Outer Join
Outer Union
Semijoin
(Division)
8.4.2. Duplikateliminierung (duplicate elimination, \(\delta\))#
Eine Duplikateliminierung wandelt eine Multimenge in eine Menge um, indem sie alle Kopien von Tupeln löscht. Sie kann auch auf Mengen angewandt werden, aber es würde das Ergebnis nicht ändern. Strenggenommen ist die Duplikateliminierung unnötig, da sie der Mengensemantik der relationalen Algebra entspricht.
\(R\)
A |
B |
C |
|---|---|---|
1 |
2 |
a |
3 |
4 |
b |
1 |
2 |
c |
1 |
2 |
d |
\(\delta(\pi_{A,B}(R))\)
A |
B |
|---|---|
1 |
2 |
3 |
4 |
8.4.3. Aggregation#
Eine Aggregation fasst die Werte einer Spalte zusammen.
Es ist eine Operation auf einer Menge oder Multimenge atomarer Werte (nicht auf Tupeln). Je nach Kontext kann die Mengensemantik oder die Multimengensemantik mehr Sinn machen.
Bei einer Aggregation gehen die Null-Werte in der Regel nicht mit in die Berechnung ein.
Wie in Excel gibt es verschiedene Aggregationsoperatoren. Je nach Datenbanksystem kann es auch weitere Operatoren geben.
Summe (SUM)
Durchschnitt (AVG)
Auch: STDDEV und VARIANCEMinimum (MIN) und Maximum (MAX)
Für nicht-numerische Werte ist es das Maximum bzw. Minimum lexikographischer Ordnung.Anzahl (COUNT)
Die doppelten Werte gehen bei der Anzahl auch doppelt ein.
Angewandt auf ein beliebiges Attribut ergibt dies die Anzahl der Tupel in der Relation.
Dabei werden Zeilen mit NULL-Werten in der Regel mitgezählt.
\(R\)
A |
B |
|---|---|
1 |
2 |
3 |
4 |
1 |
2 |
1 |
2 |
SUM(B) = 10
AVG(A) = 1,5
MIN(A) = 1
MAX(B) = 4
COUNT(A) = 4
COUNT(B) = 4
Zu den verschiedenen Aggregationen hier ein Beispiel anhand einer Film Tabelle:
Film
Titel |
Jahr |
Länge |
Typ |
StudioName |
SchauspName |
|---|---|---|---|---|---|
Total Recall |
1990 |
113 |
Farbe |
Fox |
Sharon Stone |
Basic Instinct |
1992 |
127 |
Farbe |
Disney |
Sharon Stone |
Total Recall |
1990 |
113 |
Farbe |
Fox |
Arnold |
Dead Man |
1995 |
121 |
s/w |
Paramount |
Johnny Depp |
MAX(Jahr): Jüngster Film
MIN(Länge): Kürzester Film
SUM(Länge): Summe der Filmminuten
AVG(Länge): Durchschnittliche Filmlänge
MIN(Titel): Alphabetisch erster Film
COUNT(Titel): Anzahl Filme
COUNT(StudioName): Anzahl Filme
AVG(SchauspName): syntax error
8.4.4. Gruppierung (group, \(\gamma\))#
Die Gruppierung spielt eine wichtige Rolle im Zusammenhang mit Aggregationen. Sehr oft werden für einzelne Elemente in der Relation Aggregationen durchgeführt.
Die Gruppierung ist die Partitionierung der Tupel einer Relation gemäß ihrer Werte in einem Attribut oder mehreren Attributen.
Ihr Hauptzweck ist die Aggregation auf Teilen einer Relation (Gruppen).
Beispielsweise ist eine Film Relation gegeben:
Film(Titel, Jahr, Länge, inFarbe, StudioName, ProduzentID)
Gesucht werden die Gesamtminuten pro Studio:
Gesamtminuten(StudioName, SummeMinuten)
Um das Gesuchte zu erhalten, wird zunächst nach StudioName gruppiert. Danach wird in jeder Gruppe die Länge der Filme summiert und letztendlich die Paare (Studioname, Summe) ausgegeben.
Der Operator \(\gamma\) steht für die Gruppierung. \(\gamma_L\)( R ) ist eine Gruppierung auf einer Relation R, wobei L eine Menge von Attributen ist. Ein Element in L ist entweder ein Gruppierungsattribut nach dem gruppiert wird oder ein Aggregationsoperator auf ein Attribut von R (inkl. neuen Namen für das aggregierte Attribut).
Das Ergebnis wird wie folgt konstruiert:
Die Relation R wird in Gruppen partitioniert, wobei jede Gruppe gleiche Werte im Gruppierungsattribut hat. Falls kein Gruppierungsattribut angegeben wird, ist ganz R die Gruppe
Für jede Gruppe wird ein Tupel erzeugt, mit:
Wert der Gruppierungsattribute
Aggregierte Werte über alle Tupel der Gruppe
Im Folgenden betrachten wir einige Beispiele, wie Gruppierungen verwendet werden:
Beispiel 1:
Film
Titel |
Jahr |
Länge |
Typ |
StudioName |
|---|---|---|---|---|
Total Recall |
1990 |
113 |
Farbe |
Fox |
Basic Instinct |
1992 |
127 |
Farbe |
Disney |
Dead Man |
1995 |
90 |
s/w |
Paramount |
Durchschnittliche Filmlänge pro Studio:
\(\gamma_{Studio, AVG(Länge)→Durchschnittslänge}\)(Film)
Unser Gruppenattribut ist Studio und wir aggregieren über das Attribut Länge, um den Durchschnitt zu ermitteln und benennen zuletzt AVG(Länge) zu Durchschnittslänge um
Anzahl der Filme pro Schauspieler
\(\gamma_{SchauspName, Count(Titel)→Filmanzahl}\)(Film)
Unser Gruppierungsattribut ist SchauspName und wir betrachten für jede/n Schaupspieler*in alle Filme und zählen diese, zuletzt wird für bessere Handhabung wieder unbenannt
Durchschnittliche Anzahl der Filme pro Schauspieler
\(\gamma_{AVG(Filmanzahl)}(\gamma_{SchauspName, Count(Titel)→Filmanzahl}\)(Film))
In diesem Beispiel sehen wir zwei verschachtelte Gruppierungen. Zuerst zähllen wir alle Filme pro Schauspieler*in (Ausdruck wie oben) und über die daraus resultierende Relation, berechnen wir den Durchschnitt der Filmanzahl
Als Übung können sie zu Hause die folgenden Beispiele in Ausdrücke der Relationalen Algebra umwandeln:
Anzahl Schauspieler pro Film
Durchschnittliche Anzahl der Schauspieler pro Film
Studiogründung: Kleinstes Jahr pro Studio
Beispiel 2:
Betrachten wir nun die Relation SpieltIn(Titel, Jahr, SchauspName). Wir möchten für jeden Schauspieler*in , der/die in mindestens 3 Filmen mitspielte, das Jahr des ersten Filmes.
Um das gewünschte Ergebnis zu bekommen, muss nach SchauspName gruppiert werden, danach das Minimum von Jahr und der Count von Titel gebildet werden. Anschließend selektieren wir nach Anzahl der Filme und projezieren auf SchauspName und Jahr.
\(\pi_{SchauspName, MinJahr}(\sigma_{AnzahlTitel≥3}(\gamma_{SchauspName, MIN(Jahr)→MinJahr, COUNT(Titel)→AnzahlTitel}(SpieltIn)))\)
Beispiel 3:
Wir haben erneut die Relation SpieltIn(Titel, Jahr, SchauspName) gegeben und möchten für jeden Schauspieler*in , der/die in mindestens 3 Filmen mitspielte, das Jahr des ersten Filmes und zusätzlich den Titel dieses Films. Die Idee ist genauso wie vorher in Beispiel 2. Jedoch wird anschließend ein Self-Join durchgeführt, um Filmtitel zu bekommen. Ganz zum Schluss wird nach SchauspName gruppiert, um die Gruppe auf einen Film zu reduzieren.
\(\gamma_{SchauspName, MIN(MinJahr)→MinJahr, MIN(Titel)→Titel}( (SpieltIn) ⋈_{SchauspName = SchauspName, MinJahr = Jahr}
(\pi_{SchauspName, MinJahr}(\sigma_{AnzahlTitel≥3}(
\gamma_{SchauspName, MIN(Jahr)→MinJahr, COUNT(Titel)→AnzahlTitel}(SpieltIn)
) ) )
)\)
Beispiel 4 mit komplexen Ausdrücken und Gruppierungen:
Es sind folgende Relationen gegeben:
Stud(Matrikel, Name, Semester)
Prof(ProfName, Fachgebiet, GebJahr)
VL(VL_ID, Titel, Saal)
Lehrt(ProfName, VL_ID)
Hört(Matrikel,VL_ID)
Gesucht werden die Fachgebiete von Professor*innen, die VL halten, welche weniger als drei Hörer*Innen haben. Zunächst zählen wir in der Hört-Relation die Anzahl der Matrikelnummern und selektieren, jene, die weniger als drei haben. Die resultierende Relation daraus joinen wir mit Prof und Lehrt. Anschließend gruppieren wir nach Fachgebiet. Die Gruppierung fungiert hier wie eine Projektion, es werden jedoch noch Duplikate entfernt.
Mit Gruppierung: \(\gamma_{Fachgebiet}\)( (Prof ⋈ Lehrt) ⋈ (\(\sigma_{ COUNT < 3(gVL_ID,COUNT(Matrikel)-> COUNT}\)(Hört)))
Alternativ: \(\pi_{Fachgebiet}\)( (Prof ⋈ Lehrt) ⋈ (\(\sigma_{ COUNT < 3(gVL_ID,COUNT(Matrikel)-> COUNT}\)(Hört)))
8.4.5. Sortierung (sort, \(\tau\))#
\(\tau_L\)( R ) sortiert die Realtion R, wobei L eine Attributliste aus R ist. Sei L = (A1,A2,…,An) wird zuerst nach A1, bei gleichen A1 nach A2 usw. sortiert.
Wichtig: Das Ergebnis der Sortierung ist keine Menge, sondern eine Liste. Daher sollte die Sortierung der letzte Operator eines Ausdrucks sein. Ansonsten würden wieder Mengen entstehen und die Sortierung wäre verloren. Trotzdem kann es in DBMS vorteilhaft sein manchmal auch zwischendurch zu sortieren.
8.4.6. Semi-Join (⋊)#
In den vorherigen Kapiteln haben wir den Theta- und Natural-Join kennengelernt. Nun wollen wir in den folgenden Kapiteln weitere Joinformen kennenlernen. Wir starten mit dem Semi-Join.
Formal: Wir haben die Relationen R(A) und S(B) gegeben.
R ⋉ S : = \(\pi_A\)(R⋈S)
= \(\pi_A\)( R ) ⋈\(\pi_{A\cap B}\)(S)
= R⋈\(\pi_{A\cap B}\)(S)
Ein Semi-Join ist eine Projektion der Attribute von R, hier A, auf den Natural-Join zwischen R und S. Bzw. der Join zwischen den Attributen von R und den Attributen von S, die eine Überschneidung mit denen von R haben. Zuletzt kann eine Semi-Join auch als der Join zwischen R und dem Teil von S sein, welcher eine Überschneidung mit R hat. Die Definition ist analog für Theta-Joins.
In Worten: Wir joinen R und S, aber nur die Attribute von R sind für uns von Wichtigkeit. Das Ergebnis ist nicht wieder gleich R, da wir nur jene Attribute von R ausgeben, die auch joinbar mit S sind, ohne S mitauszugeben.
Wichtig: Der Semi-Join ist natürlich nicht kommutativ: R ⋉ S ≠ S ⋉ R.
Beispiel 1
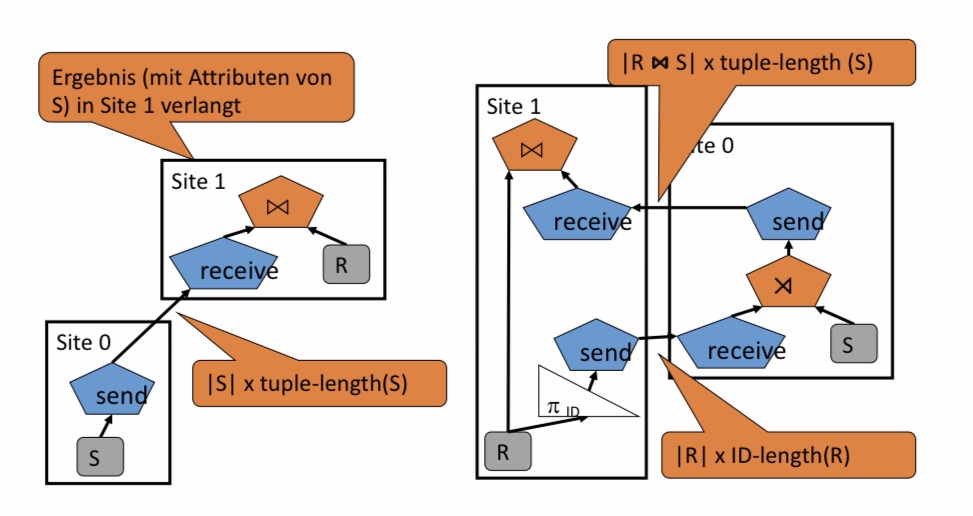
Semi-Joins sind vorallem interessant, wenn Datenbankberechnungen auf verteilten Systemen stattfinden, da so kontrolliert werden kann wie viele der Daten weitergegeben werden. Betrachten wir zur Veranschaulichung ein Beispiel. Angenommen wir haben einen Server, der die Relation R enthält und einen anderen Server, der die Relation S enthält gegeben. Nun möchten wir R ⋉ S durchführen. Eine Möglichkeit wäre es, das Site 1 die komplette Relation S anfordert und den Semi-Join dann durchführt. Jedoch interessiert uns bei S nur das Joinattribut und wir schicken, aber die gesamte Relation, also eine Größe von Länge der Daten multipliziert mit der Länge der Tupel. Ein anderer Weg wäre nur die Joinattribute von S, in diesem Beispiel ID, zu schicken, welches die Kommunikationskosten deutlich verringern würde. Hier ist natürlich vorausgesetzt, dass das System weiß, dass ein Semi-Join durchgeführt werden soll.
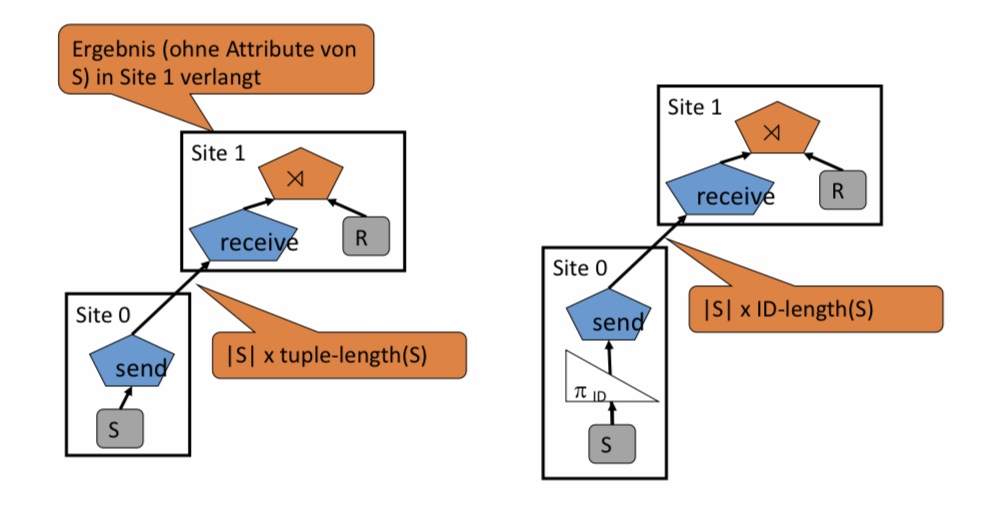
Beispiel 2
Betrachten wir nun einen “komplizierteren” Weg. Wir projezieren auf R und schicken die Joinattribute zu dem Server, auf welchem S liegt und semi-joinen diese. Nun wurde die Tupelanzahl schon verringert und wir schicken, das Ergebnis wieder zur Site 1 un joinen diese wieder mit R.
Beispiel 3
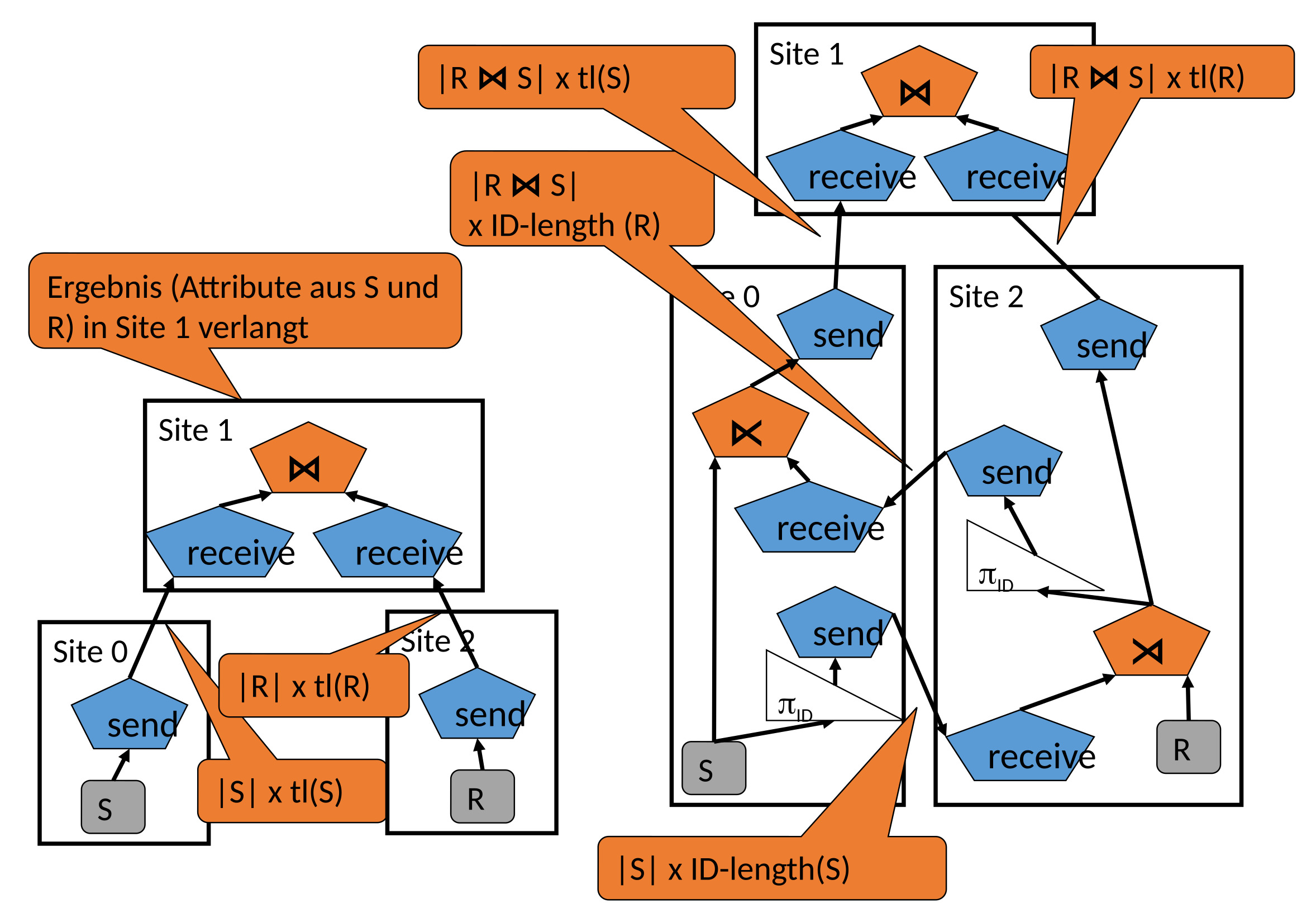
In unserem letzten Beispiel haben wir drei Server gegeben. Unser Ziel ist es, dass alle Attribute aus S und R in Site 1 enthalten sind. Der einfache Weg ist beide Relationen komplett rüberzuschicken und zu joinen. Ein anderer Weg wäre die IDs von S zum Server von R zu schicken und diese zu semi-joinen. Dann werden nur jene Tupel die joinbar mit S sind an unseren Zielserver geschickt. Zeitgleich kann ein Semi-Join zwischen S und den zu Site 0 geschickten IDs von R durchgeführt werden. Daraus resultieren jene Tupel von S die joinbar mit R sind und diese werden auf zum Zielserver geschickt. Zum Schluss werden die beiden Relationen verjoint. Die Frage die sich nun stellt, ist wie groß R und S sein müssen, s.d der “kompliziertere” Weg kostengünstiger ist.
8.4.7. Outer Joins (Äußere Verbünde, |⋈|)#
Outer-Joins fungieren so wie wir es bei normalen Joins gewohnt sind, außer das „dangling tuples“ nun in das in das Ergebnis mitaufgenommen werden und mit Nullwerten (padding) aufgefüllt werden.
Nullwert: \(\perp\) bzw. null (≠ 0)
Bei einem Full outer join werden alle Tupel beider Operanden angegeben, bei Tupel die nicht sinnvol verjoint werden können, werden die “Lücken” mit Nullwerten aufgefüllt. Schreibweise: R |⋈| S.
Bei einem Left outer join (bzw. Right outer join) werden alle Tupel des linken (bzw. rechten) Operanden übernommen, und jene die nicht verjoint werden konnten, werden ebenfalls mit Nullwerten aufgefüllt. Schreibweise: R |⋈ S (bzw. R ⋈| S)
Der herkömmlicher Join wird auch „Inner join“ genannt.
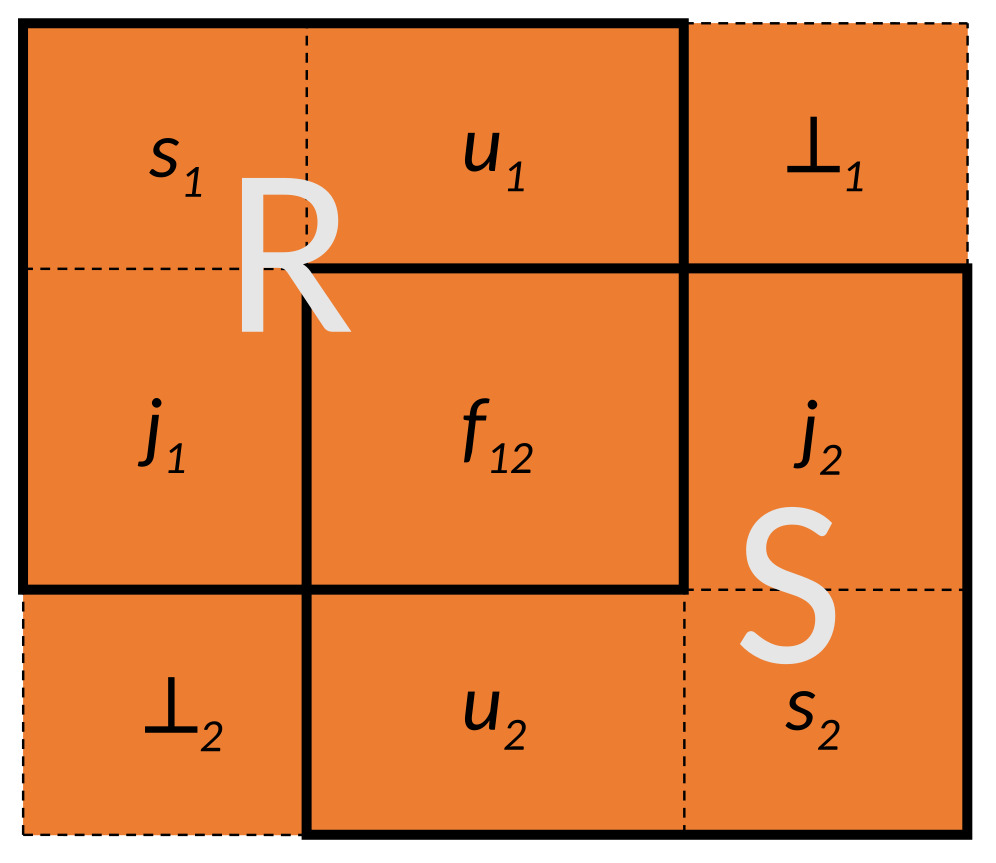
In der Veranschaulichung 1, haben wir die Relationen R uns S gegeben:R⋈S
Ergebnis besteht aus j1, f12 und j2
R |⋈ S
Ergebnis besteht aus s1, u1, \(\perp_1\), j1, f12 und j2
R ⋈| S
Ergebnis besteht aus j1, f12, j2, s2, u2, \(\perp_2\),
R |⋈| S
Alle Attribute sind enthalten
8.4.8. Outer Union (⊎)#
Beim Outer Union werden inkompatible Schemata auch vereinigt. Das Schema besteht dann aus Vereinigung der Attributmengen, wobei fehlende Werte werden mit Nullwerten ergänzt werden. In dem Beispiel unten können nur die Attribute B, C vereinigt werden. Bei den restlichen Attributen A, D wird die fehlende Spalte mit Nullwerten aufgefüllt.
|
|
\(R⊎S\)
A |
B |
C |
D |
|---|---|---|---|
1 |
2 |
3 |
\(\perp\) |
6 |
7 |
8 |
\(\perp\) |
9 |
7 |
8 |
\(\perp\) |
\(\perp\) |
2 |
5 |
6 |
\(\perp\) |
2 |
3 |
5 |
\(\perp\) |
7 |
8 |
10 |
8.4.9. Division (division, /)#
Der Divionsoperator wird typischerweise nicht als primitiver Operator unterstützt. Er kann jedoch bei speziellen Anfragen vorteilhaft sein.
Z.B möchten wir alle Segler*innen, die alle Segelboote reserviert haben finden. Hier haben wir eine Vorbedingung die gewissermaßen auf die Existenz von Tupeln in anderen Relationen voraussetzt.
Wir haben die Relation R(x,y) und die Relation S(y) gegeben.
R/S = { t \(\in\) R(x) | \(\forall\) y \(\in\) S \(\exists\) <x, y> \(\in\) R}
R dividiert durch S, gibt jene Tupel aus R zurück, wo für alle y in S es <x,y> in R gibt.
R/S enthält alle x-Tupel (Segler*\innen), so dass es für jedes y-Tupel (Boot) in S ein xy-Tupel in R gibt.
Andersherum: Falls die Menge der y-Werte (Boote), die mit einem x-Wert (Segler*in) assoziiert sind, alle y-Werte in S enthält, so ist der x-Wert in R/S.
Eine weitere Anfrage, die mit einer Division ausgedrückt werden kann ist: Hole die Namen von Angestellten, die an allen Projekten arbeiten.
Sinnvoller: Hole die Namen von Angestellten, die an allen Projekten arbeiten, in denen auch „Thomas Müller“
arbeitet.
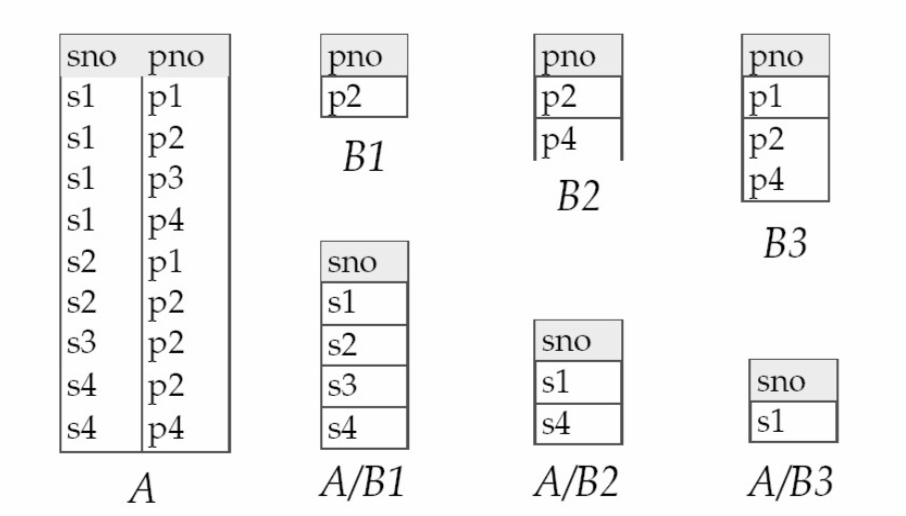
Betrachten wir folgendes Beispiel zur Division. Relation A hat die Attribute sno und pno und die Relationenn B1, B2, B3 nur das Attribut pno. A/B1 enthält alle sno’s die in A mit den pno’s aus B1 auftauchen. Der Wert p2 taucht in A mit den sno’s s1, s2, s3 und s4 auf, folglich bildet sich A/B1 daraus. Das gilt analog für A/B2 und A/B3.
Die Division ist kein essentieller Operator,sondern lediglich nur eine nützliche Abkürzung. Ebenso wie Joins, aber Joins sind so üblich, dass Systeme sie speziell unterstützen. Die Idee um R/S zu berechnen sieht wei folgt aus: Berechne alle x-Werte, die nicht durch einen y-Wert in S „disqualifiziert“ werden.
x-Wert ist disqualifiziert, falls man durch Anfügen eines y-Wertes ein xy-Tupel erhält, das nicht in R ist.
Disqualifizierte x-Werte: \(\pi_{x}\) ((\(\pi_{x}\)( R ) \(\times\) S) − R)
=> R/S: \(\pi_{x}\)( R ) − alle disqualifizierten Tupel
8.5. Fragen#
Die hier verwendete Version des Multiple-Choice-Trainers von EILD.nrw wird über GitHub-Pages gehostet und in das Skript eingebunden.
Alle Fragen und Kategorien befinden sich zurzeit in Überarbeitung und sind nicht final.
Für den vollen Funktionsumfang wird empfohlen einen auf Firefox basierten Browser zu nutzen, ansonsten können unerwünschte Nebeneffekte entstehen.

