Transaktionsmanagement
Contents
11. Transaktionsmanagement#

11.1. Motivation - Transaktionsmanagement#
Bisher haben wir in unseren Beispielen angenommen, dass nur ein Nutzer auf die Datenbank zugreift(Isolation). In der Realität werden in Betrieb genommene Datenbanken, von vielen Nutzern und Anwendungen gleichzeitig lesend und schreiben genutzt. Weiterhin haben wir angenommen, dass Anfragen und Updates aus einer einzigen atomaren Aktion bestehen, in der die DBMS nicht mitten ausfallen kann(Atomizität). Jedoch bestehen einfache Anfragen in Wahrheit oft aus mehreren Teilschritten.
11.1.1. Motivierendes Beispiel#
Betrachten wir folgendes Beispiel. Zwei Personen Philipp und Sarah teilen sich ein Konto und können dies bearbeiten. Der aktuelle Kontostand beträgt 500. In der Tabelle werden die Bearbeitungen von Philipp und Sarah dargestellt, wobei eine Zeile einen Zeitpunkt darstellt, in der Operationen ausgeführt werden.
Zuerst liest Sarah den Wert des Kontos und speichert diesen in die Variable y. Danach macht Philipp dasselbe und speichert den Wert in x. Philipp zahlt weitere 200 auf den Kontostand und commitet dies. Sarah nimmt danach 100 aus dem Konto, jedoch wird mit dem alten Kontostand 500 weitergerechnet. Der falsche Wert 400 wird commitet, obwohl auf dem Konto 600 sein sollten. Dieses Beispiel stellt einen Non-repeatble Read dar, ein Problem aus einere Reihe von Problemen, die eine DBMS in inkonsiste Zustände führen kann. Die Probleme werden wir in diesem Kapitel kennenlernen.
Kontostand: 500 |
|
|---|---|
Philipp |
Sarah |
|
read(K,y) |
read(K,x) |
|
x:=x+200 |
|
write(x,K) |
|
commit |
|
|
y:=y-100 |
|
write(y,K) |
|
commit |
Kontostand: 400 |
|
11.2. Transaktionen#
Eine Transaktion ist eine Folge von Operationen (Aktionen), die die Datenbank von einem konsistenten Zustand in einen konsistenten (eventuell veränderten) Zustand überführt, wobei das ACID-Prinzip eingehalten werden muss.
11.2.1. Transaktionen – Historie#
In alten DBMS wurde kein Formalismus über Transaktionen implementiert, sondern lediglich nur Tricks benutzt. Die ersten (ineffiziente) Implementierung von Formalismen, wurde in den 80ern von Jim Gray(ACM Turing Award), mit dem System R eingeführt. Eine weitere wichtige Person, ist C. Mohan, der im ARIES Project vom IBM Reasearch, der mit Algorithms for Recovery and Isolation Exploiting Semantics effiziente Implementierungen, insbesondere im Bereich von Transaktionen in verteilten Anwendungen und Services, entwickelt hat.
C. Mohan |
Jim Gray |
|---|---|
11.2.2. ACID#
Das ACID-Prinzip stellt die Eigenschaften einer Transaktion, es wird aus folgenden Teilprinzipien zusammengesetzt:
Atomicity (Atomarität): Eine Transaktion wird entweder ganz oder gar nicht ausgeführt.
Consistency (Konsistenz oder auch Integritätserhaltung): Die Datenbank ist vor Beginn und nach Beendigung einer Transaktion jeweils in einem konsistenten Zustand.
Isolation (Isolation): Eine Transaktion, die auf einer Datenbank arbeitet, sollte den „Eindruck“ haben, dass sie allein auf dieser Datenbank arbeitet.
Durability (Dauerhaftigkeit / Persistenz): Nach erfolgreichem Abschluss einer Transaktion, muss das Ergebnis dieser Transaktion „dauerhaft“ in der Datenbank gespeichert werden.
11.2.3. Beispielszenarien#
Einige Beispieszenarien für Probleme im Transaktionsmanagement sind z.b die Platzreservierung für Flüge aus vielen Reisebüros gelichzeitig. Ein Platz könnte mehrfach verkauft werden, wenn mehrere Reisebüros den Platz als verfügbar identifizieren. Ein weiteres Beispiel sind überschneidende Konto-Operationen einer Bank, wie im ersten Beispiel des Kapitels zu sehen ist. Auch bei statistischen Datenbankoperationen kann es zu Problemen kommen, wenn während der Berechnung Daten geändert werden, s.d. die Ergebnisse verfälscht sind.
11.2.4. Beispiel – Serialisierbarkeit#
In diesem Beispiel haben wir die Relation Fluege(Flugnummer, Datum, Sitz, besetzt) gegeben. Zusätzlich haben wir eine Funktion chooseSeat(), die nach einem freiem Platz sucht und ihn gegebenenfalls besetzt. Unten sehen Sie einen Embedded-SQL-Codeausschnitt.
EXEC SQL BEGIN DECLARE SECTION;
int flug;
char date[10];
char seat[3];
int occ;
EXEC SQL END DECLARE SECTION;
void chooseSeat() {
/* Nutzer nach Flug, Datum und Sitz fragen */
EXEC SQL SELECT besetzt INTO :occ FROM Fluege
WHERE Flugnummer=:flug
AND Datum=:date AND Sitz=:seat;
if(!occ) {
EXEC SQL UPDATE Fluege SET besetzt=TRUE
WHERE Flugnummer=:flight AND Datum=:date AND Sitz=:seat;
}
else …
}
Problematisch wird es, wenn die Funktion chooseSeat() von mehreren Usern zugleich aufgerufen wird. Wir haben User 1 und 2. User 1 findet zuerst einen leeren Platz, aber dieser besetzt ihn noch nicht. User 2 findet denselben leren Platz. Nachdem User 2 denselben leeren Platz, wie User 1 gefunden hat, besetzt User 1 diesen. Zuletzt besetzt auch User 2 diesen. Das Problem ist, dass beide User glauben den Platz reserviert zu haben. Die Lösung für diese Problem, ist das beide Transaktionen (eine Spalte stellt eine Transaktion dar) in serielle oder serialisierbare Schedules umgewandelt werden, wir wir im Weiteren kennenlernen werden.
Schedule |
|
|---|---|
User 1 findet leeren Platz |
|
|
User 2 findet leeren Platz |
User 1 besetzt Platz |
|
|
User 2 besetzt Platz |
11.2.5. Beispiel - Atomizität#
In diesem Beispiel möchten wir einen Betrag von konto1 auf konto2 überweisen. Zuerst wird überprüft, ob konto1 überhaupt genug Geld hat, um den geforderten Betrag zu überweisen. Ist dies der Fall wird der Betrag auf konto2 gutgeschrieben. Nun kann es sein, dass das System in diesem Moment abstürzt. Der Betrag wurde auf konto2 gutgeschrieben, jedoch noch nicht von konto1 abgezogen. Es ist möglich, dass die Datenbank in einen inkonsistenten Zustand hinterlassen wird. Lösung für diese Problem ist Atomizität. In diesem Fall würden die vorherigen Transaktionsschritte verworfen werden, da eine Transaktion nach dem Atomizitäts-Prinzip nur ganz oder garnicht ausgeführt wird.
EXEC SQL BEGIN SECTION;
int konto1, konto2;
int kontostand;
int betrag;
EXEC SQL END DECLARE SECTION;
void transfer() {
/* User nach Konto1, Konto2 und Betrag fragen */
EXEC SQL SELECT Stand INTO :kontostand FROM Konten
WHERE KontoNR=:konto1;
If (kontostand >= betrag) {
EXEC SQL UPDATE Konten
SET Stand=Stand+:betrag
WHERE KontoNR=:konto2;
EXEC SQL UPDATE Konten
SET Stand=Stand-:betrag
WHERE KontoNR=:konto1;
} else /* Fehlermeldung */
}
11.2.6. Probleme im Mehrbenutzerbetrieb#
In diesem Kapitel beschäftigen wir uns mit vier bekannnten Problemen, die im Mehrbenutzerbetrieb auftreten können.
Dirty Read: Abhängigkeiten von nicht freigegebenen Daten
Nonrepeatable Read: Inkonsistentes Lesen
Phantom-Problem: Berechnungen auf unvollständigen Daten
Lost Update: Verlorengegangenes Ändern
11.2.7. Dirty Read#
Wir haben zwei Transaktionen T1 und T2 gegeben. Zuerst wird in T1 aus der Tabelle A der Wert ausgelesen und in x gespeichert. Auf x wird dann 100 addiert und der Wert von x wird in die Tabelle A geschrieben. Die Transaktion T1 ist jedoch noch nicht commitet. Währenddessen werden in T2 die Werte aus den Tabellen A und B gelesen und in die Variablen x und y gespeichert. Es wird die Summe aus x und y gebildet, wobei der Wert in x aus T2 den Wert x:=x+100 aus T1 hat. Die Summe wird in T2 in die Tabelle B geschrieben und es wird commitet. Zuletzt findet ein abort in T1 statt, welches den Effekt hat, dass die vorherigen Transaktionsschritte aus T1 verworfen werden. Das Problem ist, dass T2 den veränderten A-Wert liest, diese Änderung aber nicht endgültig ist, sondern sogar ungültig.
T1 |
T2 |
|---|---|
read(A,x) |
|
x:=x+100 |
|
write(x,A) |
|
|
read(A,x) |
|
read(B,y) |
|
y:=y+x |
|
write(y,B) |
|
commit |
abort |
|
Folie nach Kai-Uwe Sattler (TU Ilmenau)
11.2.8. Nonrepeatable Read#
Im Folgenden betrachten wir ein Beispiel für Nicht-wiederholbares Lesen. In unserem Beispiel möchten wir die Zusicherung haben, dass x = A + B + C am Ende der Transaktion T1 gilt, wobei x, y, z lokale Variablen seien.
Zuerst wird in T1 der Wert aus A gelesen und in x gespeichert. Danach wird in T2 der Wert von A halbiert. Auf den Wert von C wird der neue Wert von A addiert. Die Änderungen aus T2 werden commitet. Anschließend wird in T1 der Wert aus B und C gelesen und auf x addiert. Das Problem ist, dass der Wert x in T1 nicht mehr nachvollzogen werden kann, da A sich im Laufe der Transaktion geändert hat. Zuletzt ist x = A + B + C + A/2.
T1 |
T2 |
|---|---|
read(A,x) |
|
|
read(A,y) |
|
y:=y/2 |
|
write(y,A) |
|
read(C,z) |
|
z:=z+y |
|
write(z,C) |
|
commit |
read(B,y) |
|
x:=x+y |
|
read(C,z) |
|
x:=x+z |
|
commit |
|
Beispiel nach Kai-Uwe Sattler (TU Ilmenau)
11.2.9. Das Phantom-Problem#
In diesem Beispiel haben wir ein Budget von 1000 gegeben und möchten dies gleichmäßig auf die Gehälter aller Mitarbeiter*Innen aufteilen. In T1 wird zuerst die Anzahl der Mitarbeiter*Innen in die Variable x gespeichert. Danach wird in T2 ein weiterer Mitarbeiter in die Tabelle eingefügt und commitet. Anschließend wird in T1 das Budget auf die Gehälter aller Mitarbeiter*Innen verteilt. Jedoch ist der Mitarbeiter Meier nicht in die Gehaltsabrechnung eingegangen. Tatsächlich müsste es SET Gehalt = Gehalt +10000/(X+1) sein. Meier ist das Phantom.
T1 |
T2 |
|---|---|
SELECT COUNT(*) |
|
|
INSERT INTO Mitarbeiter |
|
commit |
UPDATE Mitarbeiter |
|
commit |
|
Beispiel nach Kai-Uwe Sattler (TU Ilmenau)

11.2.10. Lost Update#
Bei diesem Beispiel für ein Lost Update, lesen T1 und T2 den Wert aus A, welcher 10 ist. T1 addiert Eins dazu und T2 addiert ebenfalls Eins dazu. Beide schreiben den Wert wieder in A. Jedoch wird die Erhöhung von T1 nicht berücksichtigt. In diesem Fall hätte man gerne die Veränderung von T1 vor dem Lesen in T2 erkannt.
T1 |
T2 |
A |
|---|---|---|
read(A,x) |
|
10 |
|
read(A,x) |
10 |
x:=x+1 |
|
10 |
|
x:=x+1 |
10 |
write(x,A) |
|
11 |
|
write(x,A) |
11 |
Folie nach Kai-Uwe Sattler (TU Ilmenau)
11.2.11. Transaktionen in SQL#
In SQL werden mehrere Operationen/Anfragen in eine Transaktion gruppiert. Ein SQL Befehl entspricht einer Transaktion. Die Transaktionen werden per Definition atomar und per SQL Standard serialisierbar ausgeführt. Diese Regeln können auch aufgeweicht werden s. Isolationsebenen. Ausgelöste TRIGGER werden ebenfalls innerhalb der Transaktion ausgeführt. Explizit kann der Beginn einer Transaktion mit START TRANSACTION deklariert werden. Das Ende einer Transaktion (falls mit START TRANSACTION gestartet), kann mit COMMIT(erfolgreiches Ende der Transaktion) oder mit ROLLBACK oder ABORT(Scheitern der Transaktion) signalisiert werden. Beim zweiten werden schon erfolgte Änderungen rückgängig gemacht. In nötigen Fällen werden von der DBMS selbst ROLLBACK oder ABORT ausgelöst, die entsprechende Fehlermeldung muss dann von der Anwendung erkannt werden.
11.2.12. Isolationsebenen#
Das Aufweichen von ACID in SQL-92 ist mit sogenannten Isolationsebenen möglich. Pro Transaktion können weniger einschränkende Regeln wie z.B read uncommited o.Ä. festgelegt werden. Die weiteren Ebenen dienen als Hilfestellung für das DBSM zu Effizienzsteigerung.
set transaction
[ { read only | read write }, ]
[isolation level {
read uncommitted |
read committed |
repeatable read |
serializable }, ]
[ diagnostics size ...]
Die Standardeinstellung ist die strengste Form und sieht wie folgt aus:
set transaction read write,
isolation level serializable
11.2.13. Bedeutung der Isolationsebenen#
read uncommitted: Diese Isolationsebene ist die schwächste Stufe und erlaubt den Zugriff auf nicht geschriebene Daten. Falls geschrieben werden soll muss read write angegeben werden, da hier ausnahmsweise der default read only ist. Durch das Weglassen von Sperren, wird die Effiezenz gesteigert, da keine Transaktionen behindert werden.
read committed: Mit dieser Isolationsebene dürfen nur endgültig geschriebene Werte gelesen werden, jedoh ist nonrepeatable read immernoch möglich.
repeatable read: Bei dieser Isolationsebene sind nonrepeatable reads verhindert, aber das Phantomproblem kann auftreten.
serializable: Bei der strengsten Isolationsebene wird Serialisierbarkeit (default) garantiert. Transaktion sehen nur Änderungen, die zu Beginn der Transaktion committed waren (und eigene Änderungen).
11.2.14. Isolationsebenen – Übersicht#
Isolationsebene |
Dirty Read |
Nonrepeatable Read |
Phantom Read |
Lost Update |
|---|---|---|---|---|
Read Uncommited |
+ |
+ |
+ |
+ |
Read Committed |
- |
+ |
+ |
- |
Repeatable Read |
- |
- |
+ |
- |
Serializable |
- |
- |
- |
- |
11.3. Serialisierbarkeit#
In diesem Kapitel beschäftigen wir uns mit der Serialisierbarkeit von Schedules.
11.3.1. Seriell vs. Parallel#
Unser Ziel ist, dass jede Transaktion, die isoliert auf einem konsistenten Zustand der Datenbank ausgeführt wird, die Datenbank wiederum in einem konsistenten Zustand hinterlässt(Korrektheit). Eine einfache Lösung aller obigen Probleme, wäre das alle Transaktion seriell, also nacheinander ausgeführt werden. Jedoch bietet parallele Ausführung Effizienvorteile, besonders bei „Long-Transactions“, die über mehrere Stunden hinweg laufen oder auch beim Zugriff auf den Cache. Daher ist es wichtig korrekte parallele Pläne(Schedules) zu finden. In diesem Kapitel werden wir lernen, dass mit korrekt serialisierbar gemeint ist.
11.3.2. Schedules#
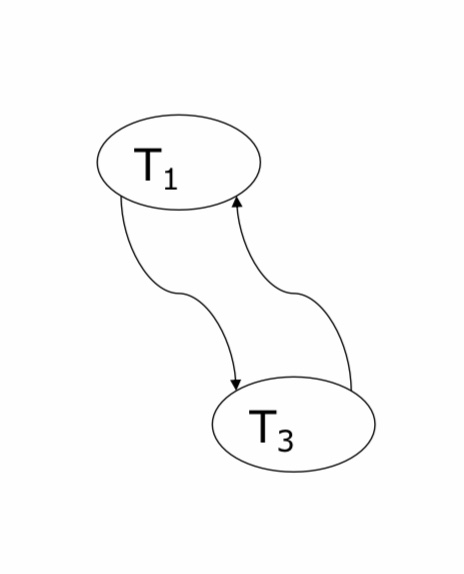
Ein Schedule ist eine geordnete Abfolge wichtiger Aktionen, die von einer oder mehreren Transaktionen durchgeführt werden. Besonders wichtige Aktionen sind READ und WRITE eines Elements. Ein „Ablaufplan“ für eine Transaktion, legt die Abfolge der jeweiligen Transaktionsoperationen fest.
Wie im unteren Beispiel zu sehen ist, fängt ein Schedule mit “Begin TA” an und endet mit einem “commit”. Wir sehen zwei Transaktionen T1 und T3, in denen jeweil lokal ein Wert aus den Variablen A und B gelesen wird. Dieser Wert wird verändert und in den Variablen überschrieben. Der Effekt dieses parallelen Schedules ist unklar. Es ist möglich, dass Updates verloren gegangen sind oder das nachdem T1 gelesen bzw. geschrieben hat ,T3 gelesen bzw. geschrieben hat.
Schritt |
T1 |
T3 |
|---|---|---|
1. |
Begin TA |
Begin TA |
2. |
read(A,a1) |
read(A,a2) |
3. |
a1 := a1 – 50 |
a2 := a2 – 100 |
4. |
write(A,a1) |
write(A,a2) |
5. |
read(B,b1) |
read(B,b2) |
6. |
b1 := b1 + 50 |
b2 := b2 + 100 |
7. |
write(B,b1) |
write(B,b2) |
8. |
commit |
commit |
Beispiel: Alfons Kemper(TU München)
11.3.2.1. Serielle und serialisierbare Schedules#
Ein serieller Schedule, ist ein Schedule in dem Transaktionen hintereinander ausgeführt werden.
Ein Schedule ist serialisierbarer, wenn ein serieller Schedule mit identischem Effekt existiert.
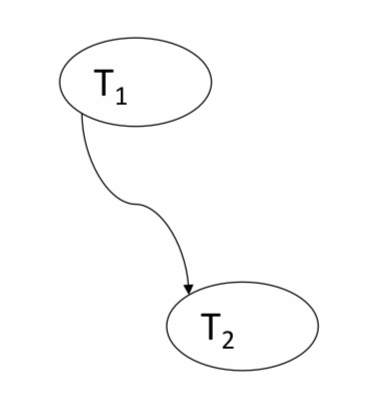
Wir sehen unten einen seriellen Schedule, in dem zuerst T1 und dann T2 ausgeführt wird. Daneben sehen wir einen nicht seriellen Schedule mit dem selben Effekt wie der serielle, also ist dieser serialisierbar.
|
|
Beispiel: Alfons Kemper(TU München)
Beispiel 2
Nun fragen wir uns, ob der folgende Schedule serialisierbar ist. Wenn wir den unteren Schedule betrachten, sehen wir ,dass die read(A)write(A) bzw. read(B)write(B) Operationen von T1 abhänging von denen von T3 sind und umgekehrt. Bei den seriellen Schedules T1,T3 und T3,T1 würden Informationen verloren gehen, daher ist der Schedule unten nicht serialisierbar.
Serialisierbar? |
|
|
|---|---|---|
Schritt |
T1 |
T3 |
1. |
BOT |
|
2. |
read(A) |
|
3. |
write(A) |
|
4. |
|
BOT |
5. |
|
read(A) |
6. |
|
write(A) |
7. |
|
read(B) |
8. |
|
write(B) |
9. |
|
commit |
10. |
read(B) |
|
11. |
write(B) |
|
12. |
commit |
|
Beispiel: Alfons Kemper(TU München)
Beispiel 2.1
Betrachten wir folgenden nicht seriellen Schedule. Zuerst wird in T1 der Wert aus A gelesen und um 50 verringert und geschrieben. Danach wird in T3 der Wert aus A gelesen und um 100 verringert und geschrieben. Folgend wird in T3 der Wert aus B gelesen und um 100 erhöht und geschrieben. Zuletzt wird in T1 der Wert aus B gelsen um 50 erhöht und geschrieben. Wir fragen uns, ob dieser Schedule serialisierbar ist?
Tatsächlich ist dieser Schedule theoretisch serialisierbar, da die Operationen von T1 und T3 aufeinander aufbauen. Es macht keinen Unterschied, ob zuerst 50 oder 100 von A abgezogen werden oder ob zuerst 50 oder 100 auf B addiert werden. Jedoch müssen wir immer vom schlimmsten Fall ausgehen und können nicht wissen, dass die Operationen aufeinander aufbauen. Daher ist der Schedule in der Realität nicht serialisierbar.
| Nicht seriell, aber serialisierbar ? | Seriell |
|
|
|---|
Beide Schedules haben den folgenden Effekt: A = A − 150, B = B + 150.
Beispiel: Alfons Kemper(TU München)
Beispiel 2.2
Dieses Beispiel ähnelt dem vorherigen, jedoch wird in T1 nur addiert und T3 wird nur multipliziert. Wenn wir nun einen seriellen Schedule wie oben erstellen, ist der Effekt nicht mehr identisch, da Punkt-vor-Strich-Rechnung eine Rolle spielt. Sowohl T1T3, als auch T3T1 haben nicht denselben Effekt. Dieses Beipiel soll nochmal veranschaulichen, dass der schlimmste Fall angenommen werden muss und der Schedule nicht serialisierbar ist.
| Schedule 1 | Schedule 2: T1T3 |
|
|
|---|
| Schedule 1 | Schedule 3: T3T1 |
|
|
|---|
Beispiel: Alfons Kemper(TU München)
Zusammenfassung Beispiel 2
Betrachten wir erneut unser Ursprungsbeispiel. Dieser Schedule ist nicht serialisierbar, denn obwohl es konkrete Beispiele solcher Transaktionen gibt, für die es einen äquivalenten seriellen Schedule gibt. Muss immer das Schlimmste angenommen.
Schritt |
T1 |
T3 |
|---|---|---|
1. |
BOT |
|
2. |
read(A) |
|
3. |
write(A) |
|
4. |
|
BOT |
5. |
|
read(A) |
6. |
|
write(A) |
7. |
|
read(B) |
8. |
|
write(B) |
9. |
|
commit |
10. |
read(B) |
|
11. |
write(B) |
|
12. |
commit |
|
Beispiel: Alfons Kemper(TU München)
Beispiel 3
Wenn wir uns nochmal die beiden seriellen Schedules T1T3 und T3T1 anschauen. Es fällt auf, dass T1T3 ≠ T3T1 ist. Hier muss nun die Applikation entscheiden, welche Reihenfolge logisch Sinn ergibt.
| Schedule 1:T1T3 | Schedule 2: T3T1 |
|
|
|---|
Beispiel: Alfons Kemper(TU München)
11.4. Konfliktserialisierbarkeit#
In diesem Kapitel wollen wir eine Methode kennenlernen, um die Serialisierbarkeit von Schedules zu überprüfen. Wir werden thematisieren wann ein Konflikt zwischen zwei oder mehr Transaktionen herrscht und wie ein äquivalenter serieller Schedule ermittelt werden kann.
11.4.1. Konflikte#
Konfliktserialisierbarkeit ist eine Bedingung für die Serilisierbarkeit und wird von den meisten DBMS verlangt (und hergestellt). Ein Konflikt herrscht zwischen zwei Aktionen eines Schedules, falls die Änderung ihrer Reihenfolge das Ergebnis verändern kann, dies passiert insbesondere bei read-/write-Operationen.
In diesem Kontext lernen wir eine neue Notation von read-/write-Operationen kennen, undzwar schreiben wir ri(x) bzw. wi(x), wobei i die TransaktionID ist und X das Datenbankelement. Mit dieser neuen Notation lassen sich Transaktionen(Sequenz solcher Aktionen) in einer Zeilenform wie z.B r1(A)w1(A)r1(B)w1(B) schreiben. Ein Schedule ist eine Menge von solchen Transaktionen in Zeilenform, welche alle Transaktionen enthalten müssen. Zudem erscheinen die Aktionen einer Transaktion im Schedule in gleicher Reihenfolge.
Angenommen wir haben die Transaktionen Ti und Tk gegegeben. Nun gelten folgende Regeln:
ri(X) und rk(X) stehen nicht in Konflikt
ri(X) und wk(Y) stehen nicht in Konflikt (falls X ≠ Y)
wi(X) und rk(Y) stehen nicht in Konflikt (falls X ≠ Y)
wi(X) und wk(Y) stehen nicht in Konflikt (falls X ≠ Y)
ri(X) und wk(X) stehen in Konflikt
wi(X) und rk(X) stehen in Konflikt
wi(X) und wk(X) stehen in Konflikt
Es gilt „No coincidences“. Man nimmt immer das schlimmste an. Die konkrete Ausprägung der write-Operationen ist egal.
Zusammenfassend kann gesagt werden, dass ein Konflikt herrscht falls zwei Aktionen das gleiche Datenbankelement betreffen und mindestens eine der beiden Aktionen ein write ist.
Haben wir einen Schedule gegeben, können wir so lange nicht-konfligierende Aktionen tauschen, bis aus dem Schedule ein serieller Schedule wird. Falls das erfolgreich ist, ist der Schedule serialisierbar.
Zwei Schedules S und S‘ heißen konfliktäquivalent, wenn die Reihenfolge aller Paare von konfligierenden Aktionen in beiden Schedules gleich ist.
Ein Schedule S ist genau dann konfliktserialisierbar, wenn S konfliktäquivalent zu einem seriellen Schedule ist.
Betrachten wir nun folgenden Schedule, bestehend aus zwei Transaktionen. Wir wollen nun den Schedule in einen seriellen Schedule umwandeln:
r1(A) w1(A) r2(A) w2(A) r2(B) w2(B) r1(B) w1(B)
Serieller Schedule T1T2:
r1(A) w1(A) r1(B) w1(B) r2(A) w2(A) r2(B) w2(B)
Serieller Schedule T2T1:
r2(A) w2(A) r2(B) w2(B) r1(A) w1(A) r1(B) w1(B)
Konflikt – konfligieren
11.4.1.1. Konfliktserialisierbarkeit vs. Serialisierbarkeit#
Wie oben genannt ist Konfliktserialisierbarkeit eine Bedingung für Serialisierbarkeit, demnach gilt Konfliktserialisierbarkeit => Serialisierbarkeit.
Betrachten wir nun den seriellen Schedule S1: w1(Y) w1(X) w2(Y) w2(X) w3(X). Der Schedule S2: w1(Y) w2(Y) w2(X) w1(X) w3(X) hat (zufällig) den gleichen Effekt wie S1 und ist also serialisierbar. Jedoch müssten konfligierende Aktionen getauscht werden, undzwar muss w1(X) vor w2(Y) getauscht werden, welches gegen die Konfliktserialisierbarkeit verstößt.
Was fällt auf? T3 überschreibt X sowieso, in dem Fall spricht man dann von Sichtserialisierbarkeit (nicht hier).
11.4.2. Graphbasierter Test#
Konfliktserialisierbarkeit kann auch graphbasiert, mittles eines Konfliktgraphen G(S) = (V,E) von Schedule S überprüft werden. Die Knotenmenge V enthält alle in S vorkommenden Transaktionen und die Kantenmenge E enthält alle gerichteten Kanten zwischen zwei konfligierenden Transaktionen. Die Kantenrichtung entspricht dem zeitlichem Ablauf im Schedule.
Nun gilt S ist ein konfliktserialisierbarer Schedule gdw. der vorliegende Konfliktgraph ein azyklischer Graph ist.
Für jeden azyklischen Graphen G(S) lässt sich ein serieller Schedule S‘ konstruieren, so dass S konfliktäquivalent zu S‘ ist, z.B mit topologischen Sortieren. Enthält der Konfliktgraph Zyklen, ist der zugehörige Schedule nicht konfliktserialisierbar.
Beispiel 1
Wir haben folgenden Schedule gegeben und möchten graphbasiert überprüfen, ob dieser konfliktserialisierbar ist. Unsere Menge V ist V={T1,T3}. Nun schauen wir anhand den obigen Regeln wo Konflikte herrschen. Wir haben einen Konflikt von write(A)(Schritt 3) zu read(A)(Schritt 5) und demnach eine Kante von T1 zu T3. Weiterhin haben wir einen Konflikt von write(B)(Schritt 8) zu read(B)(Schritt 11) und demnach eine Kante von T3 zu T1. Da unser Konfliktgraph einen Zyklus enthält, ist unser Schedule nicht konfliktserialisierbar.
| Schedule | Konfliktgraph |
|
|
|---|
Beispiel 2
Betrachten wir nun den Schedule S = r1(y) r3(u) r2(y) w1(y) w1(x) w2(x) w2(z) w3(x). Wir haben einen Konflikt von r2(y) zu w1(y), also hat unser Graph eine Kante von T2 zu T1. Dann gibt es weiterhin einen Konflikt von w1(x) zu w2(x), demnach hat unser Graph ein Kanten von T1 zu T2. Nun hat unser Konfliktgraph schon eine Zyklus und wir wissen der Schedule S ist nicht konfliktserialisierbar.
| Schedule | Konfliktgraph |
|
|
|---|
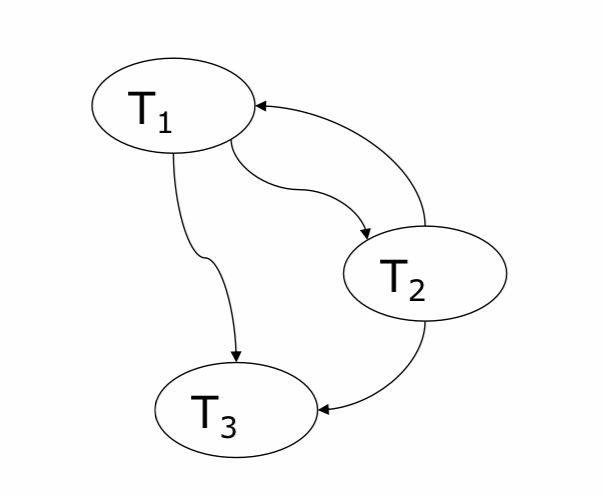
Beispiel 3
In diesem Beispiel haben wir nur einen Konflikt von T1 nach T2 und können somit schließen, dass der Schedule konfliktserialisierbar ist. Der serielle Schedule lautet T3T1. Die Reihenfolge der Transaktionen, wird anhand der Pfeilrichtungen erkannt.
| Schedule | Konfliktgraph |
|
|
|---|
Beispie: Alfons Kemper(TU München)
11.4.3. Beweis#
Nun wollen wir folgendes beweisen: Konfliktgraph ist zykelfrei <=> Schedule ist konfliktserialisierbar
Wir zeigen zeurst die eine Richtung: Konfliktgraph ist zykelfrei <= Schedule ist konfliktserialisierbar
Das ist leicht zu zeigen: Konfliktgraph hat Zykel => Schedule ist nicht konfliktserialisierbar, denn es ist nicht klar welche Transaktion zuerst ausgeführt werden soll, wie im untern Gegenbeispiel veranschaulicht.
Gegenbeispiel: T1 -> T2 -> … -> Tn -> T1
Jetzt zeigen wir die andere Richtung: Konfliktgraph ist zykelfrei => Schedule ist konfliktserialisierbar
Wir führen eine Induktion über die Anzahl n der Transaktionen durch.
n = 1: Graph und Schedule haben nur eine Transaktion. Es gibt keinen Zyklus.
n = n + 1:
Unser Graph ist zykelfrei
=> ∃ mindestens ein Knoten Ti ohne eingehende Kante.
=> ∄ Aktion einer anderen Transaktion, die vor einer Aktion in Ti ausgeführt wird und mit dieser Aktion in Konflikt steht.
Alle Aktionen aus Ti können an den Anfang bewegt werden (Reihenfolge innerhalb Ti bleibt erhalten).
D.h. der Restgraph ist wieder azyklisch (Entfernung von Kanten aus einem azyklischen Graph kann ihn nicht zyklisch machen).
Somit hat der Restgraph n-1 Transaktionen
11.5. Sperrkontrolle#
In diesem Kapitel beschäftigen wir uns wie mit Sperrkontrollen die DBMS konfliktserialisierbare Schedules garantiert.
11.5.1. Scheduler#
Der Scheduler in einem DBMS garantiert konfliktserialisierbare (also auch serialisierbare) Schedules bei gleichzeitig laufenden Transaktionen. Wenn neue Transaktionen ausgeführt werden sollen, könnte der Scheduler jedesmal einen graphbasierten Test durchführen, jedoch ist dies sehr kostenaufwendig. Stattdessen wäre es einfacher Sperren und Sperrkontrollen zu benutzte, welches in fast allen DBMS realisiert ist. Die Idee dahinter ist, dass die Transaktion für die Dauer der Bearbeitung eines Datenbankobjekts dieses sperrt, s.d. andere Transaktionen nicht darauf zugreifen können.
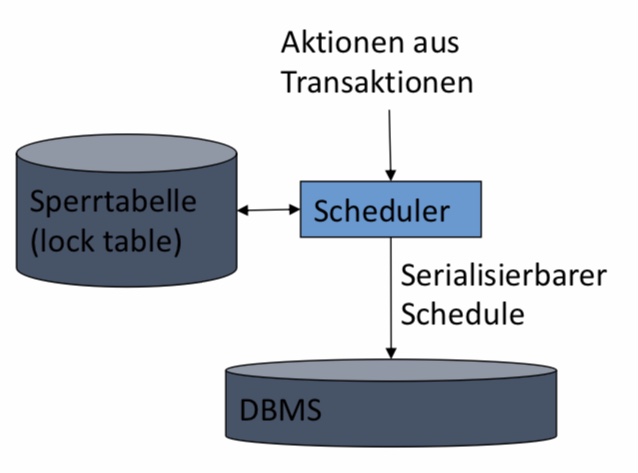
11.5.2. Sperren#
Wie oben genannte ist die Idee, dass die Transaktionen zusätzlich zu den Aktionen auch Sperren anfordern und freigeben müssen. Bedingungen hierfür sind, dass die Transaktion konsistent ist. D.h., dass Lesen oder Schreiben eines Objektes nur nachdem die Sperre angefordert wurde und bevor die Sperre wieder freigegeben wurde, erlaubt ist.
Zusätzlich muss nachdem Sperren eines Objektes muss später dessen Freigabe erfolgen. Eine weitere Bedingung ist die Legalität des Schedules, welches meint, dass zwei Transaktionen nicht gleichzeitig das gleiche Objekt sperren dürfen. In diesem Kontext lernen wir zwei neue Aktionen kennen:
li(X): Transaktion i fordert Sperre für X an (lock).
ui(X): Transaktion i gibt Sperre auf X frei (unlock).
Konsistenz: Vor jedem ri(X) oder wi(X) kommt ein li(X) (mit keinem ui(X) dazwischen) und ein ui(X) danach.
Legalität: Zwischen li(X) und lk(X) kommt immer ein ui(X)
11.5.3. Schedules mit Sperren#
Folgende zwei Transaktionen sind gegeben:
r1(A)w1(A)r1(B)w1(B)
r2(A)w2(A)r2(B)w2(B)
Wir wollen nun die Aktionen mit lock’s und unlock’s ergänzen:
l1(A)r1(A)w1(A)u1(A)l1(B)r1(B)w1(B)u1(B)
l2(A)r2(A)w2(A)u2(a)l2(B)r2(b)w2(B)u2(B)
Der Schedule der beiden Transaktionen sieht wie folgt aus:
T1 |
T2 |
|---|---|
l1(A)r1(A)w1(A)u1(A) |
|
|
l2(A)r2(A)w2(A)u2(A) |
|
l2(B)r2(B)w2(B)u2(B) |
l1(B)r1(B)w1(B)u1(B) |
|
Wir fragen uns ob der Schedule legal ist? Ja der Schedule ist legal, denn zwischen allen li(X) und lk(X) kommt immer ein ui(X).
Konfliktserialisierbar? Der Schedule ist nicht konfliktserialisierbar, denn in unserem zugehörigen Konfliktgraph gibt es eine Kante von T1 zu T2 und von T2 zu T1.
Der folgende Schedule gleicht im Grunde dem obigen. Es wird lediglich zusätzlich noch dargestellt, was für Werte die lokalen Varialen haben. Genau wie der Schedule oben, ist dieser Schedule legal, jedoch nicht serialisierbar und auch nicht konfliktserialisierbar.
T1 |
T3 |
A |
B |
|---|---|---|---|
|
|
25 |
25 |
l(A); read(A,a1) |
|
|
|
a1 := a1 + 100 |
|
125 |
|
write(A,a1); u(A) |
|
|
|
|
l(A); read(A,a2) |
|
|
|
a2 := a2 * 2 |
250 |
|
|
write(A,a2); u(A) |
|
|
|
l(B); read(B,b2) |
|
|
|
b2 := b2 * 2 |
|
50 |
|
write(B,b2); u(B) |
|
|
l(B); read(B,b1) |
|
|
|
b1 := b1 + 100 |
|
150 |
|
write(B,b1); u(B) |
|
|
11.5.4. Freigabe durch Scheduler#
Um das Problem aus dem vorherigen Kapitel zu lösen, ist dasnn alle Sperren vor den Entsperren ausgeführt werden.
Unsere alte Transaktionen:
– l1(A)r1(A)w1(A)u1(A)l1(B)r1(B)w1(B)u1(B)
– l2(A)r2(A)w2(A)u2(A)l2(B)r2(B)w2(B)u2(B)
In unseren neuen Transaktionen sind alle Sperren vor Entsperren:
– l1(A)r1(A)w1(A)l1(B)u1(A)r1(B)w1(B)u1(B)
– l2(A)r2(A)w2(A)l2(B)u2(A)r2(B)w2(B)u2(B)
Somit ist unser Schedule konsistent und legal.
Der Scheduler gibt Objektefrei und vergibt nur Sperren, wenn keine andere Sperre existiert. Die Sperrinformation werden von dem Scheduler in einer Sperrtabelle gespeichert.
11.5.5. Schedules mit Sperren#
Im Vergleich zu dem Schedule oben wird hier erst B von T1 gesperrt und dann A entsperrt. Danach wird A von T3 gesperrt und es wird auf A geschrieben. T3 fordert nun die Sperre von B an, das wird jedoch abgelehnt, da B noch von T1 gesperrt wird. Anschließend schreibt T1 auf B und gibt diese frei und zuletzt kann T3 auf B schreiben. Dieser Schedule ist legal, da alle Sperren von Entsperren stattfinden. Dieser Schedule ist ebenfalls serilialisierbar und konfliktserialisierbar, da der zueghörige Konfliktgraph azyklisch ist.
T1 |
T3 |
A |
B |
|---|---|---|---|
|
|
25 |
25 |
l(A); read(A,a1) |
|
|
|
a1 := a1 + 100 |
|
125 |
|
write(A,a1); l(B); u(A) |
|
|
|
|
l(A); read(A,a2) |
|
|
|
a2 := a2 * 2 |
250 |
|
|
write(A,a2); |
|
|
|
l(B); abgelehnt! |
|
|
read(B,b1) |
|
|
|
b1 := b1 + 100 |
|
|
125 |
write(B,b1); u(B) |
|
|
|
|
l(B); u(A); read(B,b2) |
|
|
|
b2 := b2 * 2 |
|
250 |
|
write(B,b2); u(B) |
|
|
11.5.6. 2-Phasen Sperrprotokoll#
2-Phase-Locking (2PL) ist eine einfache Bedingung an Transaktionen, nicht an den Schedule, die Konfliktserialisierbarkeit garantiert. Es besteht aus zwei Phasen:
Phase 1: Sperrphase
Phase 2: Freigabephase
So geschehen alle Sperranforderungen vor allen Sperrfreigaben.
11.5.6.1. 2-Phasen Sperrprotokoll – Beispiel#
| Schedule ohne 2-Phasen Sperrprotokoll | Schedule mit 2-Phasen Sperrprotokoll |
|
|
|---|
11.5.6.2. Deadlocks unter 2PL möglich#
Leider sind unter 2PL nicht alle Probleme gelöst, denn ein 2PL-konformer Schedule kann immernoch Deadlocks hervorrufen, wie im unteren Schedule zu sehen ist.
T1: l(A); r(A); A:=A+100; w(A); l(B); u(A); r(B); B:=B-100; w(B); u(B)
T4: l(B); r(B); B:=B*2; w(B); l(A); u(B); r(A); A:=A*2; w(A); u(A)
Zunächst sperrt T1 A und schreibt auf A. Danach sperrt T4 B und schreibt auf B. Folgend möchte T1 auf B schreiben, dies wird abgelehnt, da T4 B gesperrt hat. T4 möchte nun auch A schreiben, jedoch ist A noch von T1 besetzt. Nun haben wir ein Deadlock, denn beide Transaktionen warten auf die Freigaben des anderen. Eine mögliche Lösung ist das Einsetzten von Timeouts oder es können „Waits-for“-Graph benutzt werden. |T1|T4|A|B| |—|—|—|—| |||25|25| |l(A); read(A,a1)|||| ||l(B); read(B,b2)||| |a1 := a1 + 100|||| ||b2 := b2 * 2||| |write(A,a1)||125|| ||write(B,b2)||50| |l(B) – abgelehnt|||| ||l(A) – abgelehnt|||
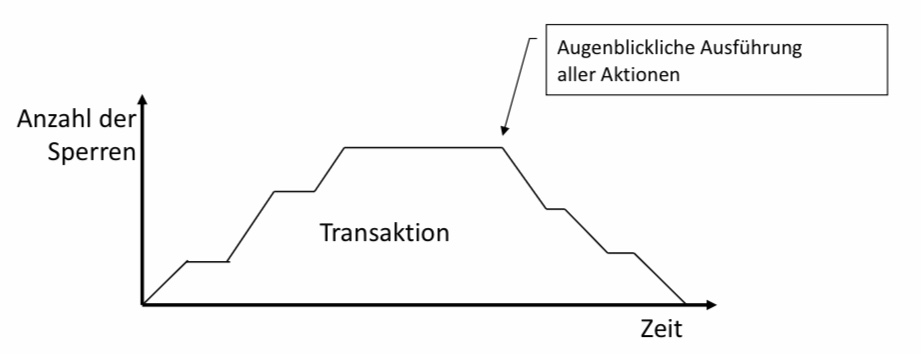
11.5.6.3. 2PL – Intuition#
Die Intuition hinter 2Pl ist, dass in der Reihenfolge des äquivalenten seriellen Schedules, zuerst die Transaktion kommt, welche als Erstes Sperren freigibt. Jede Transaktion führt sämtliche Aktionen in dem Augenblick aus, zu dem das erste Objekt freigegeben wird.
11.5.6.4. 2PL – Beweis#
Nun wollen wir dies auch beweisen. Die Idee ist, dass wir einen beliebigen, legalen Schedule S aus konsistenten, 2PL Transaktionen in einen konfliktäquivalenten seriellen Schedule konvertieren.
Wir führen eine Induktion über die Anzahl der Transaktionen n durch.
n = 1: Schedule S ist bereits seriell
n = n + 1: Enthalte S die Transaktionen T1, T2, …, Tn.
Sei Ti die Transaktion mit der ersten Freigabe ui(X).
Wir behaupten: Es ist möglich, alle Aktionen der Transaktion an den Anfang des Schedules zu bewegen, ohne konfligierende Aktionen zu passieren.
Nun nehmen wir an, dass es eine Schreibaktion wi(Y) gibt, die man nicht verschieben kann:
– … wk(Y) … uk(Y) … li(Y) … wi(Y) …
Da Ti die erste freigebenden Transaktion ist, gibt es ein ui(X) vor uk(Y):
– … wk(Y) … ui(X) … uk(Y) … li(Y) … wi(Y) …
Dasselbe gilt analog für eine Leseaktion ri(Y).
Somit ist Ti nicht 2PL.
11.5.7. Mehrere Sperrmodi#
Die Idee hinter mehreren Arten von Sperren ist, dass so die Flexibilität erhöht wird und die Menge der abgewiesenen Sperren verringert wird.
Z.B sind Sperren obwohl nur gelesen wird übertrieben.Eine gewisse Sperre ist dennoch nötig, aber mehrere Transaktionen sollen auch gleichzeitig lesen können. Für Leseoperationen können sogenannte shared locks si(X) angefordert werden. Diese erlaubt dann das Lesen für die Transaktion Ti und sperrt zudem auch den Schreibzugriff für alle anderen Transaktionen. Für Schreiboperationen wir eine exclusive lock xli(X) angefordert, welches das Lesen und Schreiben durch Transaktion Ti erlaubt. Um diese beiden Sperren aufzuheben wird wie schon bekannt einfach ein unlock ui(X) angefordert. Was die Kompabilität angeht, darf es für ein Objekt nur eine Schreibsperre oder mehrere Lesesperren geben.
11.5.8. Bedingungen#
Um die Konsistenz von Transaktionen zu wahren ist Schreiben ohne Schreibsperre und Lesen ohne irgendeine Sperre nicht erlaubt. Ebenso muss jede Sperre irgendwann freigegeben werden.
Mit den Speermodi hat sich bei der 2PL-Konformität von Transaktionen nichts geändert. Wie zuvor auch dürfen nach der ersten Freigabe keine Sperren mehr angefordert werden.
Was die Legalität von Schedules betrifft, darf es auf ein Objekt mit einer Schreibsperre keine andere Sperre einer anderen Transaktion geben und auf ein Objekt kann es mehrere Lesesperren geben. Die untere Tabelle stellt nocheinmal die Kompabilität der verschiedenen Sperren dar.
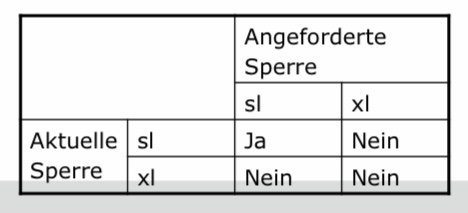
Beispiel
T1 sperrt zunächst A mit einem sharedlock, T2 tut dem ebenso und sperrt zusätzlich noch B. Folgend fordert T1 ein exclusive lock an B, jedoch ist B mit einem shared lock von T2 besetzt, weshalb die Anfrage abgelehnt wird. T2 gibt A und B frei. Zuletzt wird von T1 erneut ein exclusive lock an B angefordert und T1 liest und schreibt auf B. Ganz zum Schluss werden die Sperren von T1 freigegeben.
T1: sl1(A)r1(A)xl1(B)r1(B)w1(B)u1(A)u1(B)
T2: sl2(A)r2(A)sl2(B)r2(B)u2(A)u2(B)
Konsistent? Ja der Beispielschedule ist konsistent
2PL? Ja der Beispielschedule ist 2PL-konform
T1 |
T2 |
|---|---|
sl(A); r(A) |
|
|
sl(A)r(A) |
|
sl(B)r(B) |
xl(B) – abgelehnt! |
|
|
u(A)u(B) |
xl(B)r(B)w(B) |
|
u(A)u(B) |
|
11.5.9. Weitere Sperrarten#
Eine weitere Sperrart ist Upgraden einer Sperre von einer Lesesperre zu einer Schreibsperre, anstatt gleich strenge Schreibsperre zu setzen. Es ist auch möglich Updatesperren zu setzten, diese erlaubt nur lesenden Zugriff, jedoch kann ein Upgrade erfahren. Die klassische Lesesperre kann dann keinen Upgrade erfahren. Eine Inkrementsperre erlaubt lesenden Zugriff und erlaubt schreibenden Zugriff, falls der Wert nur inkrementiert (oder dekrementiert) wird. Dies ist erlaubt da Inkremente kommutativ sind, also sind Vertauschung erlaubt.
11.6. Fragen#
Die hier verwendete Version des Multiple-Choice-Trainers von EILD.nrw wird über GitHub-Pages gehostet und in das Skript eingebunden.
Alle Fragen und Kategorien befinden sich zurzeit in Überarbeitung und sind nicht final.
Für den vollen Funktionsumfang wird empfohlen einen auf Firefox basierten Browser zu nutzen, ansonsten können unerwünschte Nebeneffekte entstehen.